¿Cuáles son las alternativas al modelo de Black-Scholes que no asumen comportamiento de paseo aleatorio?

Question

Recientemente he comenzado a operar en opciones binarias como hobby y quiero saber cómo deciden los corredores las tasas de retorno en las opciones binarias. Hice esta Pregunta y probé el modelo propuesto en la respuesta. Funciona bien en mercados sintéticos con volatilidad constante. (un corredor que ofrece esto es deriv).

Pero al intentar predecir la tasa de retorno del corredor en un mercado real como forex, no logra hacerlo. Asumo que esto se debe a que los corredores no utilizan Black-Scholes para predecir los precios de opciones no binarias debido a sus suposiciones de caminata aleatoria.

¿Cuáles son las alternativas al modelo Black-Scholes y hay una forma de incorporar movimientos de tendencia en este modelo?

Answer 1

Con respecto a un comentario que hiciste; ¿cómo puedes estar seguro de que lo demás está correcto si tu valor está tan equivocado? Con FX, hay dos tasas de interés, los IVs suelen cotizarse en delta (frecuentemente ajustados por prima), y tienes el problema de la moneda nominal y la moneda de prima en diferentes denominaciones (Ccy1 y Ccy2 respectivamente) por ejemplo.

Recomiendo mirar libros básicos introductorios sobre precios de opciones como:

• Opciones, Futuros y Otros Derivados, John Hull
• Conceptos y Prácticas de Finanzas Matemáticas, Mark Joshi
• Paul Wilmott sobre Finanzas Cuantitativas, Paul Wilmott
• Teoría de Arbitraje en Tiempo Continuo, Tomas Björk
• Volatilidad y Precios de Opciones, Sheldon Natenberg

Para FX, puedo recomendar altamente:

• Precios de Opciones de Cambio, Iain J. Clark
• Riesgo de Sonrisa en Opciones de FX, Antonio Castagna
• Opciones de FX y Productos Estructurados, Uwe Wystup

En pocas palabras, el precio de las opciones se basa enteramente en argumentos de "sin arbitraje" y de "replicación / cobertura" dentro de un marco neutral de riesgo. Como resultado, el precio del derivado no depende de la deriva / tendencia del precio de la acción. Tampoco puedes implementar el modelo de manera diferente porque constantemente abrirías oportunidades de arbitraje.

En el mundo simple de Black Scholes (generalmente llamado Garman Kohlhagen en FX), aún tienes muchos matices con los que lidiar. La mayoría de las operaciones de opciones de FX son OTC, y las comillas vienen en IVOL directamente (ATM Delta Neutral Straddles, Risk Reversals y Butterflies para varios deltas). El delta mismo puede ser ajustado por prima o excluido, así como a término o spot. En cuanto a la comilla (EURUSD es CCY1CCY2, lo que significa 1 EUR por cuántos USD), tienes la nominal en CCY1, la prima en CCY2, todo lo demás requiere que tengas en cuenta el cambio de numerario, como se muestraaquí con código. Para ser preciso, también necesitas distinguir entre la fecha de precio y la fecha de prima.

Cómo se calculan las opciones estándar de vainilla se muestra aquí.

Como se menciona en laotra respuesta, en el mundo plan vol Black-Scholes (BS) usando la notación BS habitual, el precio justo de la opción de efectivo o nada es e^(rt)*N(d2) que es laprobabilidad descontada de la opción venciendo in the money.

Para calcular esto enJulia, todo lo que necesitas es este código:

using Distributions, Dates   

N(x) = cdf(Normal(0,1),x)

# Fwd
function GKF(F,K,t_d,t_e, ccy2, )
    d1 = ( log(F/K) +  0.5*^2*t_e ) / (*sqrt(t_e))
    d2 = d1 - *sqrt(t_e)
    c  = exp(-ccy2*t_d)*(F*N(d1) - K*N(d2)) 
    return c, exp(-ccy2*t_d)*N(d2)
end

donde t_d y t_e son el tiempo de entrega y el tiempo de vencimiento. El resto es lógica estándar de Black Scholes, y utilicé el forward para evitar tener que calcular la segunda tasa de interés menos líquida, que a menudo se implícita a partir de la paridad de tasas de interés cubierta para hacer que el modelo sea internamente consistente y libre de arbitraje.

Usando datos de mercado y convirtiendo la tasa de interés libre de riesgo en un analógico continuo se ve así.

ccy2 = 0.0007897 # USD
 = 6.747/100.

price_dt = Date(2020,12,30)
premium_dt = Date(2021,01,04)
expiry_dt = Date(2021,3,31)
delivery_dt = Date(2021,4,06)
days_to_expiry = (expiry_dt - price_dt) 
days_to_delivery = (delivery_dt - premium_dt) 

r2_cont = log(1+ccy2*days_to_delivery.value/360)/(days_to_delivery.value/365)

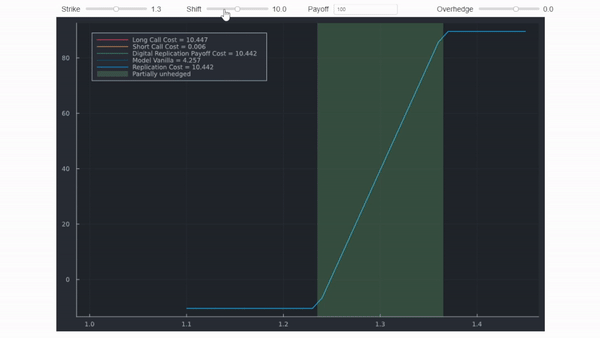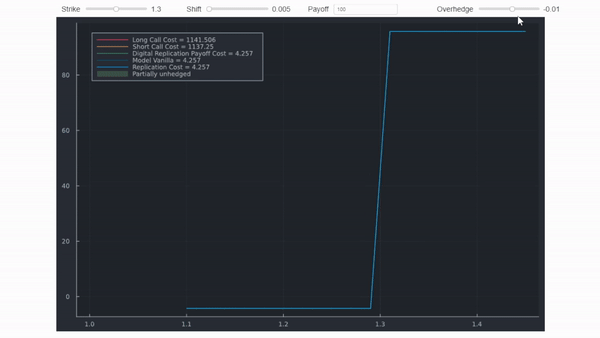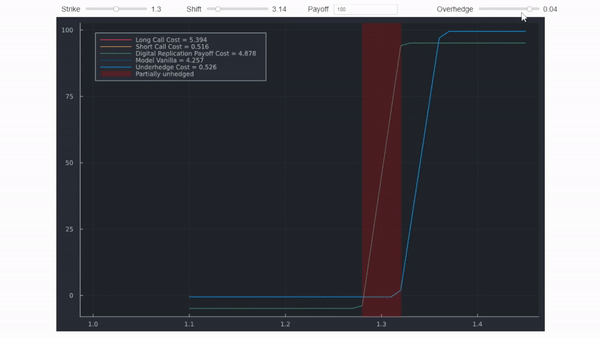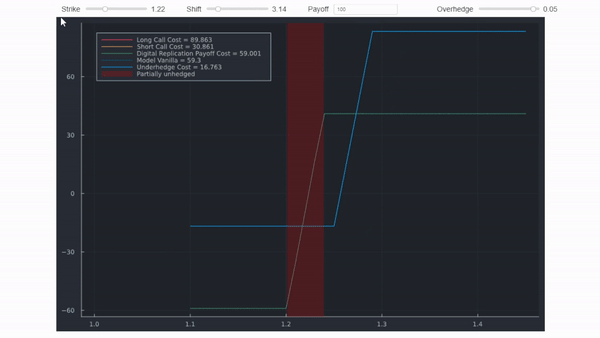
Eso es todo realmente. En entornos del mundo real, siguiendo la lógica de sin arbitraje y replicación, a los practicantes del mercado les gusta encontrar maneras de replicar pagos. Por ejemplo, al igual que los swaps de varianza tienen una replicación teórica, el pago de los digitales puede replicarse con un spread de opción de compra ajustado para capturar la asimetría. Por ejemplo, estableciendo los strikes en ± = ±1/2. Mi respuesta a tu primera pregunta utilizó una figura que muestra que una sobrecobertura costará más que la cobertura centrada en el strike de barrera, porque su pago es estrictamente mayor. Como se mencionó, hay detalles que se omiten en esta figura (los diagramas de pago se desplazarían ligeramente, reflejando diferentes costos por la prima). La gif a continuación mostrará la misma información pero usa cálculos precisos que coinciden con la replicación de Bloomberg a continuación. Utiliza spreads y desplazamientos irrealistas para hacer clara la distinción.

Por otro lado, esto es más complicado. El beneficio es que te permite tener en cuenta la asimetría IV. En general, la diferencia de precio será marginal y es seguro evitar esto. También será difícil de implementar porque implica ajustar una superficie de volatilidad. Si intentas hacerlo, estos son los pasos:

• Calcula el spread

  function spread(K,shift)
        lower_K = K*(1-shift/2)
        upper_K = K*(1+shift/2)
        spread  = upper_K-lower_K
        return lower_K, upper_K, spread
    end
  
        strike = 1.22 
    spr = spread(strike,0.01) 
    val = ("Lower","Upper","Spread") 
    k = Dict(zip(val,spr))

• Calcula el ajuste de notional necesario porque el spread pagará la diferencia entre el strike más bajo y más alto solamente. El spread entre los strikes * Notional es la suma de los pagos.

   function notional_adj(N,spread,payoff)
        return payoff/(spread*N) end

• Obtén las vols ajustadas para el spread de la superficie de volatilidad (generalmente obtenidas a través de una lógica como se muestraaquí por ejemplo). Utilicé la API de Bloomberg para obtener los IV necesarios para el spread. El pricer en sí mismo (OVML) solo muestra la volatilidad básica.

  \= Dict("Mid" => 6.747/100, "Lower" => 6.78047/100, "Upper" => 6.73819/100)

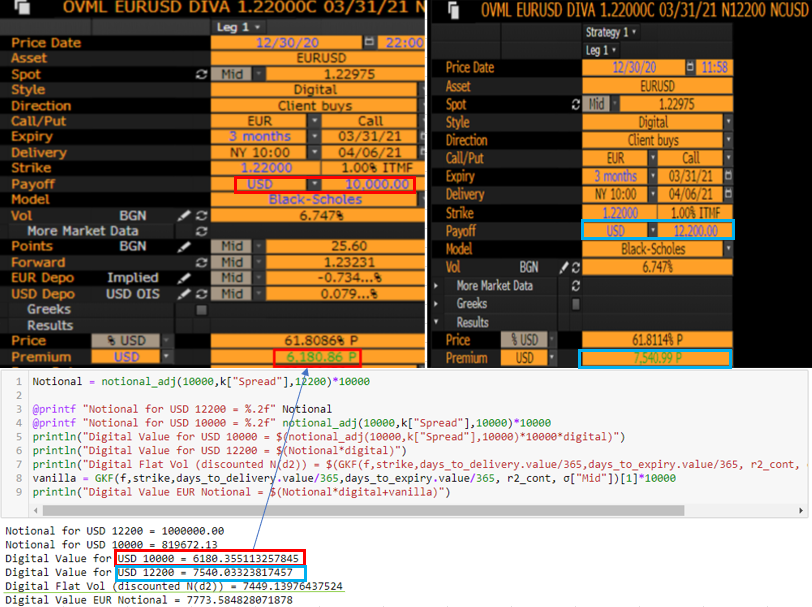
• Obtén los resultados y compáralos con Bloomberg:

Puedes ver que el Notional necesario fue de aproximadamente ~ 819.6K y 1M para esos pequeños digitales de efectivo o nada y un spread del 1%. No coincide perfectamente con BBG, pero la diferencia es menor a 1 USD. Además, la diferencia con el mundo del Black-Scholes (BS) de volatilidad plana es solo ~ 90 Euros.

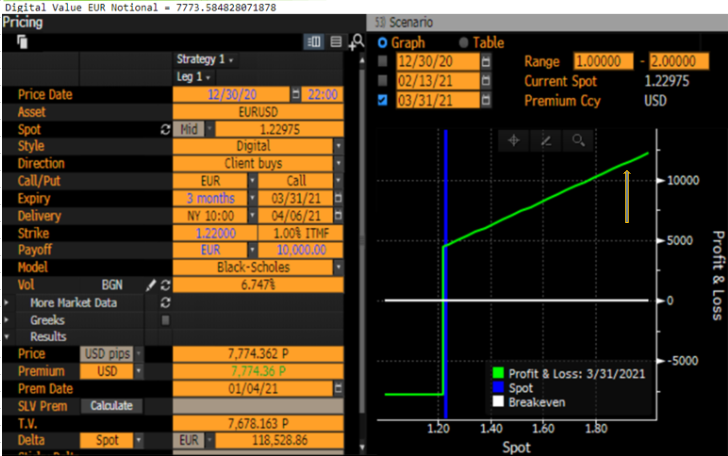
En el caso del notional en EUR, tienes otro problema, a saber, que ya no es un efectivo o nada, sino una opción binaria de activo o nada. La tasa de cambio final importará para tu pago real en este caso, por lo que está escalado por una opción de compra de vanilla y la captura de pantalla de BBG muestra una pendiente ascendente en la pestaña de escenarios sobre el strike.