¿Cómo se utiliza el teorema fundamental de la fijación de precios de los activos?

Question

Sé que un modelo de mercado multiperiodo es completo y libre de arbitraje si hay un medida única equivalente de martingala . El caso es que no tengo ni idea de cómo aplicar este teorema a un simple árbol binomial. No entiendo qué tienen que ver ambas cosas.

Por ejemplo, considere:

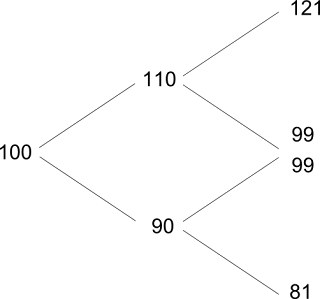
Sí, sé que $u = 1.1$ . Sé que $d = 0.9$ . Pero, ¿qué tiene que ver esto con el complicado teorema que habla de las expectativas condicionales y las medidas de martingala equivalentes? Supongo que $q = (R - d)/(u-d)$ y $1 - q$ es esta medida de martingala equivalente, pero ¿por qué? ¿Y por qué es única?

Answer 1

Bien resolver el valor de $q$ que hace que el valor de la acción dividido por el bono sea una martingala. Verás que sólo un valor lo hace. Es el que has publicado.

Si se define entonces el valor descontado de una opción como su expectativa de pago descontada, su valor descontado es una martingala.

Así que el valor descontado de todo es una martingala. Los arbitrajes no pueden ser martingalas ya que una martingala de valor inicial cero tiene una expectativa cero. Así que no hay arbitrajes bajo la medida q. Pero el conjunto de arbitrajes no cambia con la probabilidad, así que no hay arbitrajes bajo ninguna medida equivalente.

(mi libro "Conceptos" trata este tema con todo lujo de detalles).

Answer 2

Sabemos que el modelo de mercado está libre de arbitraje si y sólo si existe una medida de martingala $Q$ también el Modelo Binomial está libre de arbitraje si y sólo si $d\le 1+R\le u\,\,$ ( Teoría del arbitraje en tiempo continuo Es fácil calcular las probabilidades de la martingala. Esta condición equivale a decir que $1 + R$ es una combinación convexa de $u$ y $d$ es decir $$1+R=u\,{{q}_{u}}+d\,{{q}_{d}}$$ Por otro lado $\,{{q}_{d}}+{{q}_{u}}=1$ entonces $$\left\{ \begin{align} & u\,{{q}_{u}}+d\,{{q}_{d}}=1+R \\ & {{q}_{u}}+\,{{q}_{d}}=1 \\ \end{align} \right.$$ $$\Rightarrow \left\{ \begin{align} & {{q}_{u}}=\frac{\left| \begin{matrix} 1+R & d \\ 1 & 1 \\ \end{matrix} \right|}{\left| \begin{matrix} u & d \\ 1 & 1 \\ \end{matrix} \right|}=\frac{1+R-d}{u-d} \\ & {{q}_{d}}=\frac{\left| \begin{matrix} u & 1+R \\ 1 & 1 \\ \end{matrix} \right|}{\left| \begin{matrix} u & d \\ 1 & 1 \\ \end{matrix} \right|}=\frac{u-(1+R)}{u-d} \\ \end{align} \right.$$

(También puede leer la segunda edición de El libro de Joshi Es tan bueno).