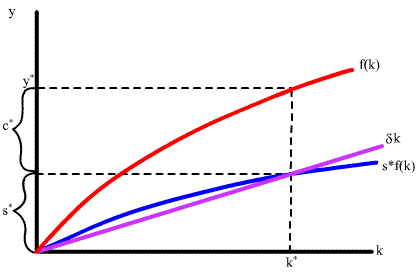
Considera una versión muy simple del modelo de Solow con tiempo discreto, un tamaño de población fijo y sin progreso tecnológico (una descripción más detallada de las suposiciones se describe aquí). El capital está en 'estado estacionario' cuando la cantidad total de depreciación iguala la cantidad total de ahorro; gráficamente, esto ocurre en la intersección de las funciones azul y morada a continuación:
Considera el proceso de ajuste al estado estacionario. A menudo he escuchado afirmar que cuanto menor sea el capital inicial, mayor será el crecimiento. Por lo tanto, el modelo predice que los países pobres crecerán más rápido que los países ricos, asumiendo que estos países son iguales en todos los demás aspectos ('convergencia condicional'). Sin embargo, al observar el gráfico aquí, parece que en un nivel muy bajo de capital, el crecimiento en realidad será muy lento. La razón es que la función de ahorro (azul) apenas supera la línea de depreciación (morada), por lo que el aumento en el capital es pequeño. A medida que el capital aumenta, la brecha entre estas funciones aumenta, por lo que la tasa de crecimiento debería aumentar. Sin embargo, eventualmente, la brecha comienza a disminuir, y el crecimiento efectivamente se desacelera (como comúnmente se afirma).
Por supuesto, he estado discutiendo la tasa de crecimiento en el capital, mientras que nos interesa la tasa de crecimiento en la producción. Y de hecho, el producto marginal de capital disminuye de forma monótona a medida que el capital aumenta. ¿Es esto lo que garantiza que la tasa de crecimiento en el capital siempre esté disminuyendo? ¿O todavía hay un período en el que la tasa de crecimiento en la producción esté aumentando?