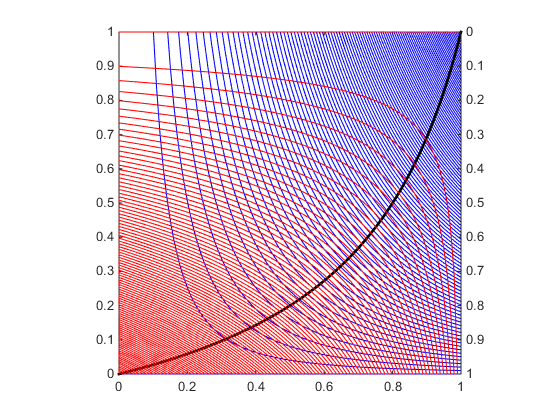
Escribí un programa tonto donde solo arreglas el endowment e=(e1,e2) y las funciones de utilidad u=(u1(x1,y1),u2(x2,y2)). El ejemplo ofrece una ilustración para tus funciones de utilidad y x1+x2=1 y y1+y2=1. He dibujado 100 curvas de indiferencia en una cuadrícula equiespaciada de niveles de utilidad dados ˉu1∈[u1(0,0),u1(1,1)] (azul) y ˉu2∈[u2(0,0),u2(1,1)] (rojo). La línea negra es la curva de contrato.
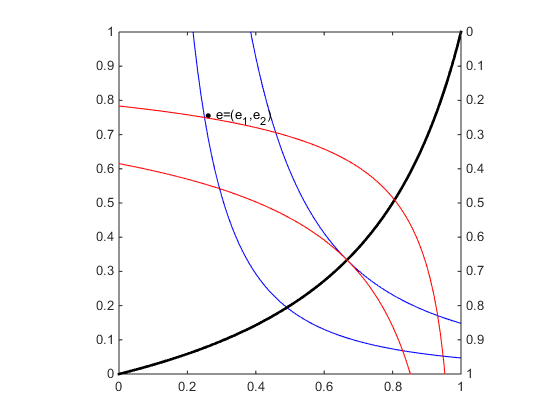
Agregué una segunda figura con algo de endowment inicial e1=(0.25,0.75), e2=(0.75,0.25) y núcleo.
![enter image description here]()
![enter image description here]()
e1 = [0.25 0.75];
e2 = [0.75 0.25];
X = 0.0:0.01:(e1(1)+e2(1));
Y = 0.0:0.01:(e1(2)+e2(2));
syms x1 y1 x2 y2 u1_bar u2_bar
u1 = x1.^2*y1;
u2 = x2*y2.^2;
I1_fun = matlabFunction(solve(u1_bar == u1, y1, 'PrincipalValue', true));
I2_fun = matlabFunction(solve(u2_bar == u2, y2, 'PrincipalValue', true));
u1_x = diff(u1, x1);
u1_y = diff(u1, y1);
u2_x = diff(u2, x2);
u2_y = diff(u2, y2);
u2_x = subs(u2_x, [x2,y2], [X(end) - x1, Y(end) - y1]);
u2_y = subs(u2_y, [x2,y2], [X(end) - x1, Y(end) - y1]);
contract_curve = matlabFunction(solve(u1_y/u1_x == u2_y/u2_x, y1));
u1_min = double(subs(u1, [x1,y1], [X(1), Y(1)]));
u1_max = double(subs(u1, [x1,y1], [X(end), Y(end)]));
u1_Array = linspace(u1_min, u1_max, 100);
I1_Array = zeros(length(X), length(u1_Array));
for i = 1:length(u1_Array)
I1_Array(:,i) = I1_fun(u1_Array(i), X);
end
u2_min = double(subs(u2, [x2,y2], [X(1), Y(1)]));
u2_max = double(subs(u2, [x2,y2], [X(end), Y(end)]));
u2_Array = linspace(u2_min, u2_max, 100);
I2_Array = zeros(length(X), length(u2_Array));
for i = 1:length(u2_Array)
I2_Array(:,i) = I2_fun(u2_Array(i), X);
end
hold on
[AX, H1, H2] = plotyy(X, I1_Array, 1-X, I2_Array)
set(AX(:),'YLim',[0 1]);
set(AX(:),'YTick',[0:0.1:1])
set(H1(1:length(u1_Array)), 'Color', 'b');
set(H2(1:length(u2_Array)), 'Color', 'r');
set(AX(2),'YDir','reverse')
axis(AX,'square')
%str1 = '\bullet e=(e_1,e_2)';
%text(e1(1),e1(2),str1)
plot(X, contract_curve(X), 'k', 'linewidth', 2)
hold off

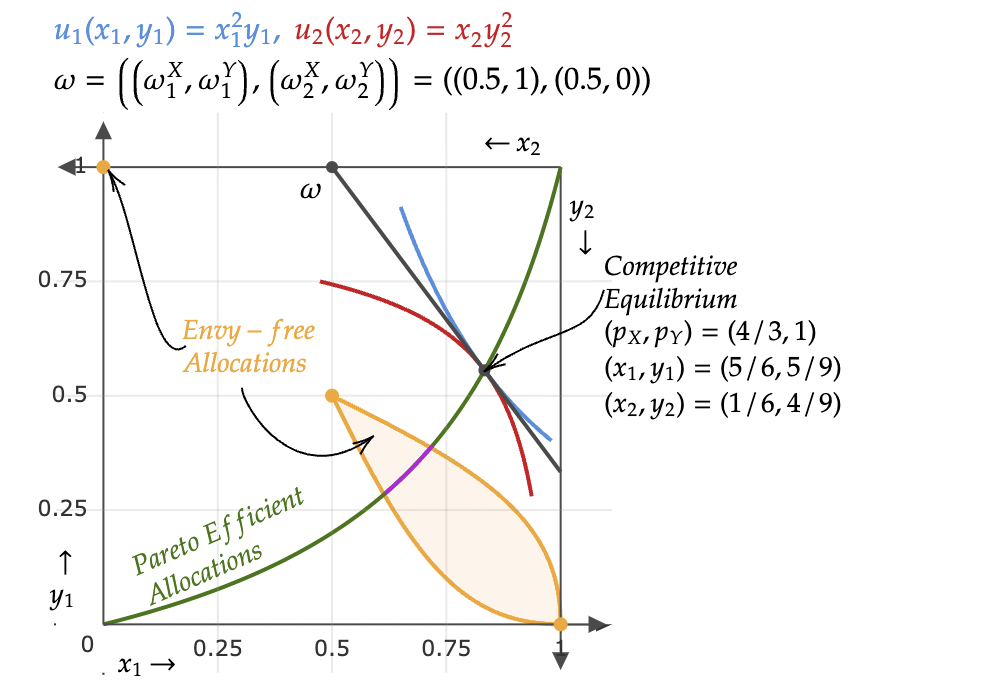


0 votos
¿Te importaría proporcionar un ejemplo específico? En general, si puedes hacer el álgebra de forma simbólica, entonces no debería ser muy difícil escribir un programa simple en, por ejemplo, Matlab que maneje expresiones simbólicas.
0 votos
@clueless sí, no es difícil, pero hay muchos detalles y pensé que alguien debía haberlo hecho antes.