Fórmula de Garman-Kohlhagen (Black-Scholes) vs. Calculadora OVML de Bloomberg

Question

Estoy tratando de ponerle precio a una opción de compra europea en USDJPY. Tenemos que $S = 112.79, K = 112.24, \sigma = 6.887\%, r_d = 1.422\%, r_f = -0.519\%, T = 0.25$. Mi modelo, basado en Black-Scholes, devuelve el valor $c = 2.149$.

Además, el precio de la opción de venta es $p = 1.055$ y se cumple la paridad put-call. Estoy seguro de que mi modelo es correcto. Sin embargo, Bloomberg, que también utiliza el modelo de Black-Scholes, devuelve el resultado (para $1M nominal) como 121.107 pips o 1.3594%P.

¿Cómo puedo llegar a un valor aproximado al generado en Bloomberg a partir de mi valor $c$?

¡Gracias de antemano!

Answer 1

Mejor tarde que nunca.

Existen muchos matices a considerar al establecer precios para las opciones. El servicio de asistencia debería haber sido capaz de orientarte hacia una solución. No creo que puedan (ser capaces de) replicar completamente, pero al menos deberían proporcionar ejemplos genéricos.

Personalmente, no me gusta la distinción entre doméstico y extranjero. Tiende a causar confusión en mi humilde opinión. Usaré CCY1CCY2 (USDJPY). Garman-Kohlhagen (abreviado GK) utiliza los términos doméstico y extranjero en sus definiciones. Se cotiza en unidades de moneda doméstica por unidad de moneda extranjera. Por lo tanto, el USD es extranjero y el JPY doméstico, como señaló rbonallo.

Por ejemplo.

• es poco probable que tu tiempo sea exactamente 0.25 (la volatilidad FX tiene un límite, y además, está la distinción entre el tiempo de vencimiento y de entrega)
• las tasas mostradas normalmente no son continuas; mientras que Garman-Kohlhagen requiere tasas continuas
• por defecto, la tasa de JPY se deduciría a través de la paridad de tipos de interés cubierta (resuelto para la tasa de JPY aquí ($r_{ccy2}$) para ser internamente consistente $$f(s,ccy1,ccy2,t) = s*exp^{(r_{ccy2}-r_{ccy1})*t}$$
• GK está valorado en términos de nominal en ccy1, y prima en ccy2
• la llamada está en perspectiva de ccy1
• OVML tiene muchos más decimales bajo el capó: los ajustes te permiten mostrar una mayor precisión, que debería ser visible al pasar el cursor sobre los valores

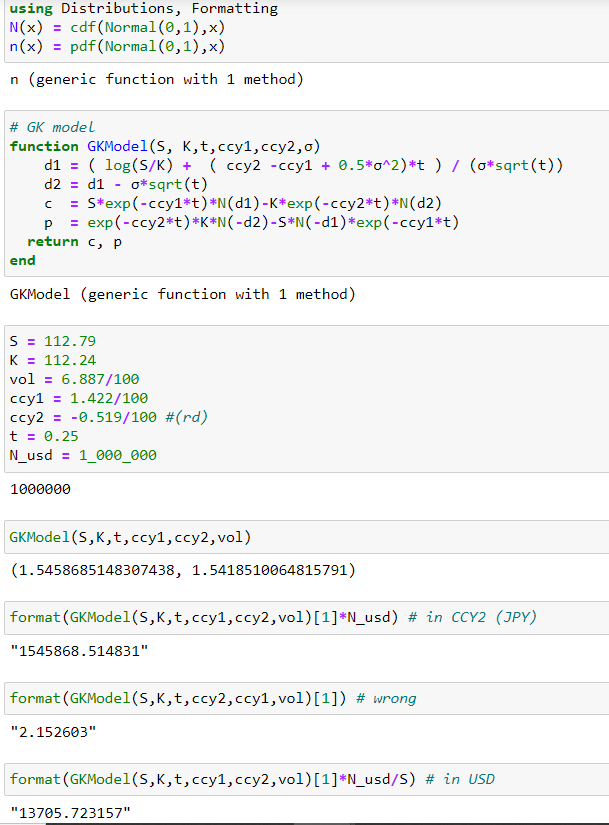
De cualquier manera, ignorando todo esto, y simplemente introduciendo tus valores en el terminal obtienes ~1.5M JPY. Mostrar el resultado en USD da lo que proporcionó rbonallo. Cerca de 121 pips USD (13.66K USD por defecto para un nominal de 1 millón de USD). Esto es 1.37% P (para pagar) en USD. Ligeramente diferente a tus valores, pero simplemente utilicé el valor a 3 meses de hoy, estaba sobrescribiendo los valores e ignoré la comilla de tipos de interés, etc.

$$= *xp^{_{1}*}*(1) *xp^{_{2}*} *(_2)$$
No estoy escribiendo esto aquí, pero lo codifiqué en Julia. Lo siguiente ignora todos los detalles mencionados anteriormente, por lo que NO coincide exactamente. Si deseas un cálculo exacto, puedes ver aquí cómo funcionan las tasas implícitas y el cálculo de días en la valoración de opciones FX.

No puedes simplemente dividir entre el spot (como preguntas en tu edición) porque tu valor se deriva mezclando tasas de interés(ver imagen: #equívocado). Si pasas de JPY a prima USD, ahí es donde entra el spot (ver imagen nuevamente).

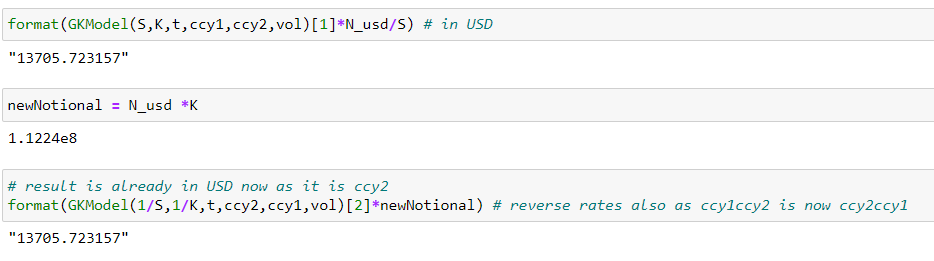
Para hacer hincapié en esto, si invirtieras esto (usaras JPYUSD) ahora tienes el nominal en JPY y la prima en USD, así como una llamada en JPY. Para obtener el mismo resultado, valoras un put en JPY, donde [2] en el código extrae el segundo argumento en la función de retorno que es el valor del put.

Put en JPY = Call en USD  

Además, necesitas tener en cuenta que tu nominal ahora está realmente en JPY. Para ajustar esto, necesitas usar el Strike (no el Spot), ya que eso es lo que realmente intercambias.

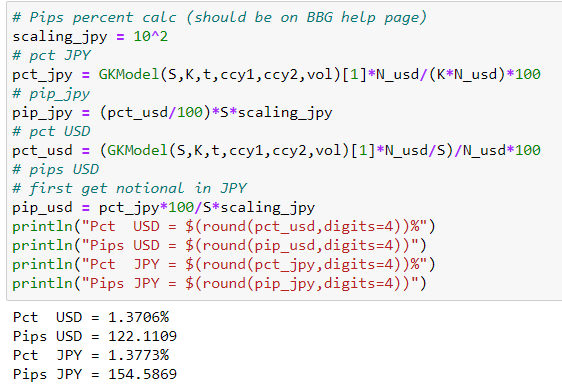
Convertir Pct en Pips es otra historia separada.

Answer 2

Para USDJPY, la convención se considera comprar dólares, vender yenes, por lo que la tasa extranjera (aquella en la que estamos comprando) sería el dólar y la doméstica (aquella en la que estamos pagando) es el yen. El precio de estos valores devuelve aproximadamente C = 121 pips de USD, ~13K USD en un nocional de $1M