Considere la lectura del excelente libro de Lorenzo Bergomi - o al menos el primer capítulo disponible aquí para su descarga -, te ayudará a aclarar las cosas.
Algunas observaciones sobre tu pregunta original:
- Es bien sabido que, bajo un supuesto de difusión pura, el total de P&L de una opción europea delta-hedgeada (es decir, una opción cuyo pago solo depende del valor del activo subyacente en una fecha futura $T$), sobre el horizonte $[0,T]$ se escribe: $$ P\&L_{[0,T]} = \int_0^T \frac{1}{2} \underbrace{\Gamma(t,S_t,\sigma^2_{t,\text{impl.}})S_t^2}_{\text{dólares de Gamma}}( \sigma^2_{t,\text{real.}} - \sigma^2_{t,\text{impl.}}) dt $$ Por lo tanto, aunque una cartera de opciones europeas delta-hedgeadas es sensible a la discrepancia de volatilidades realizada vs. implícita, no es un comercio de volatilidad puro: el término de dólares de Gamma introduce una dependencia en la trayectoria del spot. Este término de dólares de Gamma debe verse realmente como una especie de acumulador de volatilidad: solo a lo largo de las trayectorias donde el término de dólares de Gamma es distinto de cero, la discrepancia entre volatilidades realizadas e implícitas importará.
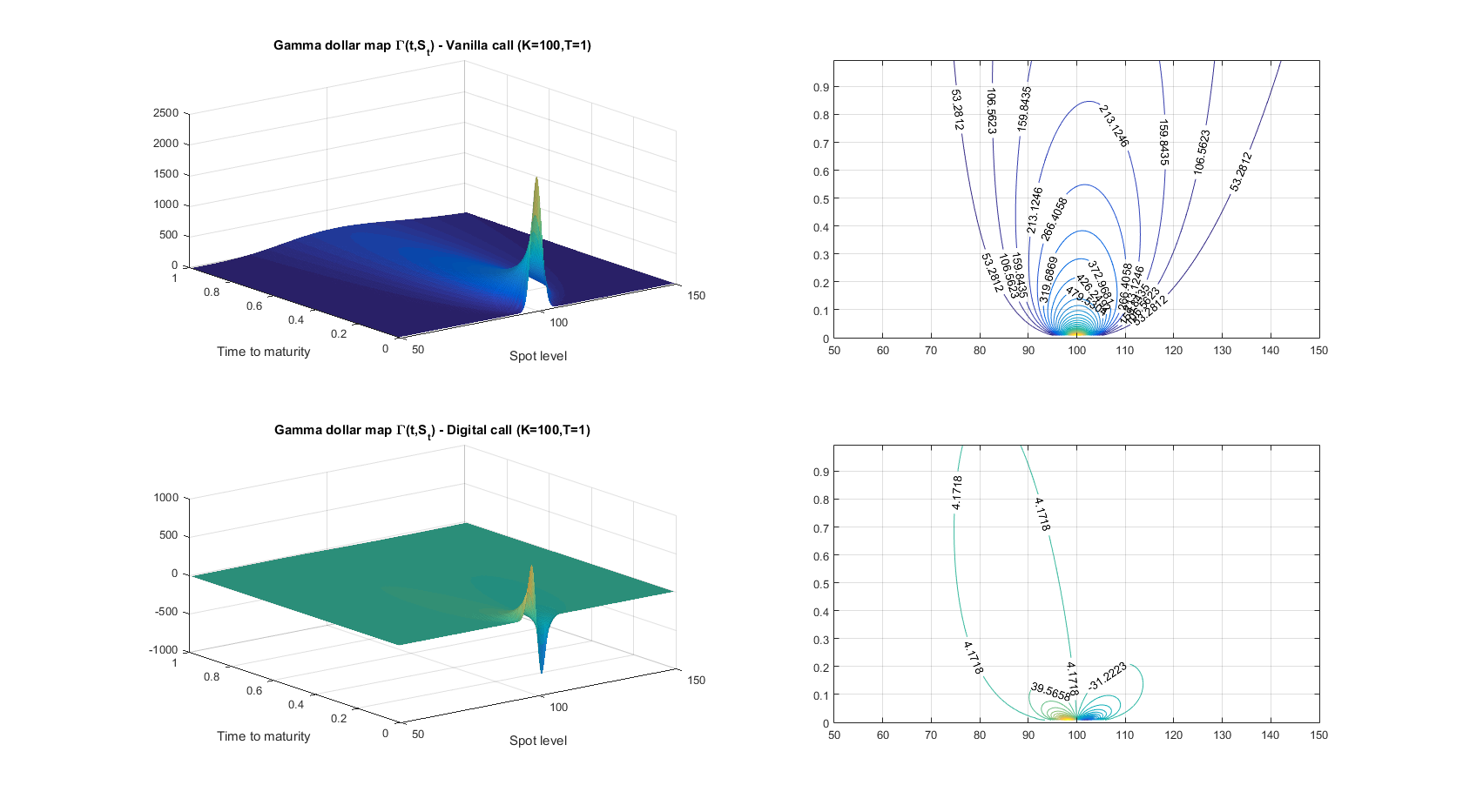
- La relación anterior sigue siendo válida para opciones digitales (o binarias), ya que también son opciones europeas después de todo. Lo que observas es simplemente una consecuencia del hecho de que el mapa de Gamma de una llamada binaria es bastante diferente al de una llamada vanilla (ver abajo): de hecho, es cero en la mayoría del dominio del tiempo hasta vencimiento/spot. Por lo tanto, la contribución de las discrepancias de volatilidad realizada vs. implícita al total de P&L es completamente diferente: solo lo que sucede (1) alrededor del strike, (2) cerca del vencimiento importa. Es por esto que no observaste una fuerte correlación entre el P&L resultante y la volatilidad realizada en todo el horizonte de delta-hedging.
![ingresar descripción de la imagen aquí]()
Ahora, con respecto al delta-hedging de opciones exóticas, citando del "resumen del capítulo" de Lorenzo Bergomi y agregando algunas de mis propias observaciones:
El delta-hedging elimina la contribución de primer orden de $\delta S$ al P&L de una posición de opción.
Aunque la expectativa del P&L de una cartera delta-hedgeada es cero (si anticipas correctamente la volatilidad - o varianza - de los rendimientos futuros),
El delta-hedging no es adecuado para reducir la desviación estándar del P&L [...] Las fuentes de dispersión de este P&L son: (a) las colas de los rendimientos, (b) la volatilidad de la volatilidad realizada y la correlación de las volatilidades realizadas futuras.
Utilizando opciones para el gamma-hedging (...)
En otras palabras, utilizando otras opciones vanilla para cancelar localmente el término de dólares de Gamma,
nos inmuniza contra la volatilidad realizada (...) El comercio dinámico de opciones vanilla, sin embargo, nos expone a la incertidumbre sobre los niveles futuros de las volatilidades implícitas.
Por lo tanto, la necesidad de modelos de volatilidad estocástica para modelar la dinámica de la volatilidad implícita.
Las opciones exóticas a menudo dependen de una manera compleja de la dinámica de las volatilidades implícitas
Una exposición que generalmente se maneja operando con opciones vanilla. Vea, por ejemplo, el caso de una llamada forward-start (relativa) en el dinero en un modelo de difusión homogénea. En ese caso muy específico, ya no nos importa el delta-hedging, ya que solo importa la dinámica de la volatilidad forward. Uno puede querer neutralizar tal exposición utilizando spreads de calendario.



0 votos
Estoy seguro de que intentan cubrirse de alguna manera, pero es mucho más difícil hacerlo y sospecho que la cobertura es menos efectiva, es decir, más riesgo idiosincrático se transmite. El concepto general es el mismo.
2 votos
Sí, en general estoy seguro de que tienes razón, pero ¿cuál es el PROPÓSITO de cobertura de opciones exóticas? Con opciones vainilla, el propósito del delta hedging es obtener ganancias de la volatilidad y no de los movimientos direccionales de precios. Lo mismo no parece aplicarse a las opciones exóticas. Estoy ejecutando algunas simulaciones en Matlab y veo que al coberturar un opción binaria, aparentemente la ganancia NO está fuertemente correlacionada con la volatilidad realizada. De hecho, no veo ninguna relación discernible entre la volatilidad realizada y la ganancia en absoluto.
0 votos
@AlexOckenden ¿Qué quieres decir con modelo de precios?