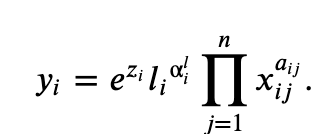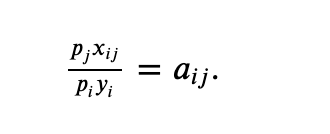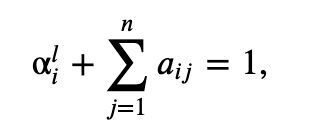Buscando las restricciones para un programa de maximización de beneficios en Acemoglu et al, 2016

Question

He estado leyendo el artículo de Acemoglu et al., 2016 Redes y la macroeconomía: una exploración empírica, y he estado luchando con un programa de maximización en las primeras páginas del artículo. Incluso si entiendo las siguientes partes, estoy un poco frustrado de no poder demostrar uno de los primeros resultados.

La función de producción es :

Con $x_{ij}$ los productos de la empresa $j$ tratados como insumo para la producción de la empresa $i$.

Mi pregunta es la siguiente : ¿Qué debo tomar como restricción para mi función Lagrangiana ? Estoy teniendo dificultades para ver cómo los autores llegaron a la conclusión (4) :

Creo que la restricción está dada por la relación

Pero debo admitir que no estoy seguro de mi resultado con estas restricciones.

¿Alguien podría darme un consejo sobre las restricciones y cómo demostrar la relación $(4)$ ?

Answer 1

El FOC es un resultado de un problema de maximización de beneficios. Los beneficios son

$$ \Pi = \underbrace{p_iy_i}_{\text{Ingresos Totales}} - \underbrace{\left(\sum_j p_jx_{ij} + wl_i\right)}_{\text{Costos Totales}} $$ Diferenciando lo anterior con respecto a $x_{ij}$ y estableciéndolo en cero te da la ecuación que estás buscando. La suposición de que los exponentes suman uno en tu última ecuación es simplemente asumir que la función de producción tiene rendimientos constantes a escala, ver aquí.