Creo que tu respuesta es realmente engañosa. El uso del estándar Black Scholes (Garman Kohlhagen) no te dará los valores ni para la prima ni para el delta, utilizando los datos de entrada y los parámetros de comercio que proporcionaste.
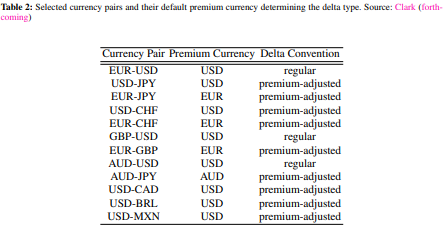
Dado que el FX es todo OTC, nunca puedes estar seguro sobre los detalles a menos que le preguntes a tu corredor. Generalmente, para mantener la liquidez, hay una serie de convenciones estandarizadas. Desafortunadamente, estas convenciones varían entre pares de divisas. Por lo general, las opciones vainilla EURUSD no están ajustadas por prima. Si tienes acceso a Bloomberg, puedes consultar en OVDV - 92) Settings->Conventions. Wystup and Reiswich, 2009 también tienen una visión general de las convenciones más comúnmente utilizadas.
![enter image description here]()
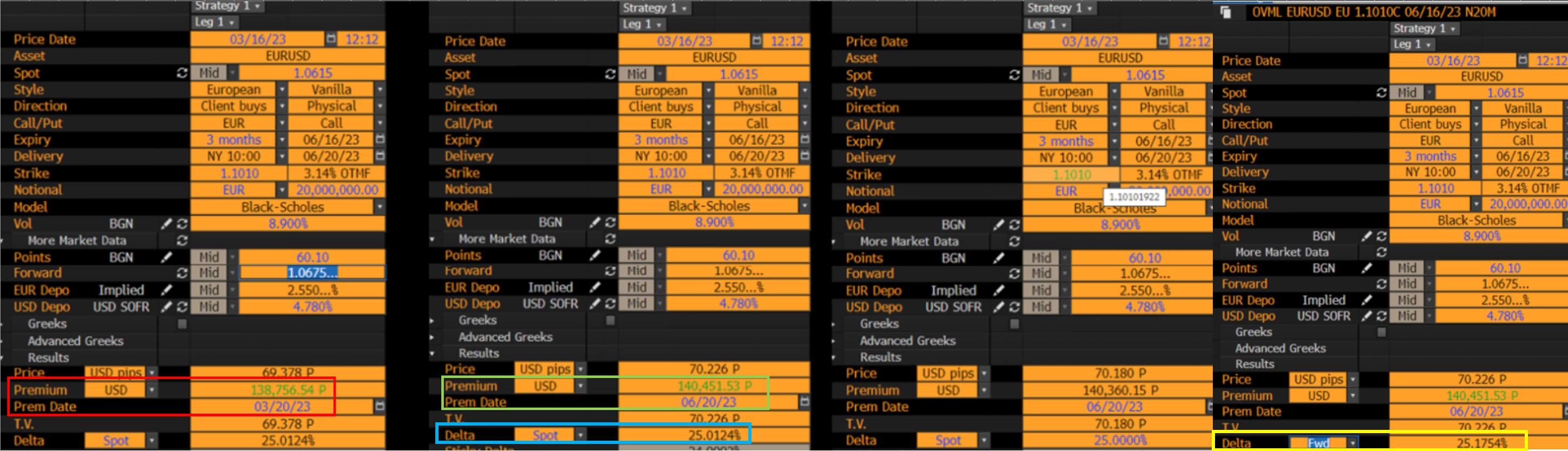
Observa la siguiente captura de pantalla de OVML de Bloomberg, donde la 3ra captura de pantalla tiene 25D como entrada y resuelve el strike (los decimales exactos se muestran en blanco - cuando pasas el cursor sobre el valor en la pantalla de OVML).
![enter image description here]()
Los valores son fáciles de replicar:
- Para CCY1CCY 2, tienes Nominal en CCY1 (20MM) y Prima en CCY2 (USD)
- Tienes una prima diferida (a futuro), por lo tanto uso dos fechas (ver aquí para una explicación)
- todos los demás datos de entrada están dados
- El modelo es simplemente el estándar Garman Kohlhagen
- todos los datos de entrada están proporcionados en la pregunta
En Julia, esto se ve de la siguiente manera:
# cargar paquetes
using Distributions, Dates, DataFrames, PrettyTables
# definir funciones auxiliares
ppf(x) = quantile(Normal(0.0, 1.0),x)
N(x) = cdf(Normal(0,1),x)
# definir GK
function GK(F,K, days_to_expiry, days_to_delivery ,ccy1, ccy2,)
d1 = ( log(F/K) + 0.5*^2*days_to_expiry/365 ) / (*sqrt(days_to_expiry/365))
d2 = d1 - *sqrt(days_to_expiry/365)
c = exp(-ccy2*days_to_delivery/365)*(F*N(d1) - K*N(d2))
_spot = exp(-ccy1*days_to_expiry/365) * N(d1)
_fwd = N(d1)
return c, _fwd, _spot
end
Todos los datos de entrada están dados, pero los días hasta el vencimiento y la entrega se calculan. Permito horas hasta el vencimiento pero eso es irrelevante aquí (el precio calculado está por debajo del cotizado, y el delta aumentaría con el tiempo creciente).
# datos de entrada
s = 1.0615
pts = 60.1
fwd_scale = 10^4
f = s + pts / fwd_scale
println("Forward = $f")
k = 1.101
= 0.089
ccy1 = 0.0255008 #0.0255 # EUR
ccy2 = 0.0478 # USD
price_dt = Date(2023,3,16)
premium_dt = Date(2023,6,20)
expiry_dt = Date(2023,6,16)
delivery_dt = Date(2023,6,20)
hours = 0 #0.7115 allows to get more accurate pricing but more hours to expiry would be needed (increases delta)
days_to_expiry = (expiry_dt - price_dt).value + hours/24
days_to_delivery = (delivery_dt - premium_dt).value + hours/24
r1_cont = log(1+ccy1*days_to_expiry/360)/(days_to_expiry/365)
r2_cont = log(1+ccy2*days_to_expiry/360)/(days_to_expiry/365)
Estoy omitiendo el formateo de PrettyTables. Básicamente, calculo el strike para 25D según Wystup and Reiswich, 2009 (omitir la bandera de call/put porque solo nos importan las calls aquí):
$$ K = fe^{-N^{-1}(e^{rf\tau} * \delta_{s})*\sigma* \sqrt{t} + \frac{1}{2}*\sigma^{2}*\tau }$$ o para delta a futuro: $$ K = fe^{-N^{-1}(\delta_{f})*\sigma* \sqrt{t} + \frac{1}{2}*\sigma^{2}*\tau }$$
= 0.25
# calcular el strike a partir del delta
k_25D = f*exp((1/2)*^2*days_to_expiry/365 - ppf(*exp(r1_cont *days_to_expiry/365))**sqrt(days_to_expiry/365))
# obtener el valor de la opción para el strike calculado y el strike cotizado
opt = [GK(f, strike, days_to_expiry, days_to_delivery, r1_cont, r2_cont, ) for strike in (k, k_25D)]
# obtener la prima spot
premium_dt_spot = Date(2023,3,20)
days_to_delivery_spot = (delivery_dt - premium_dt_spot).value + hours/24
opt2 = [GK(f, strike, days_to_expiry, days_to_delivery_spot, r1_cont, r2_cont, ) for strike in (k, k_25D)];
Notional = 20_000_000
df = DataFrame("Strike" => [k, k_25D],
"Fwd Premium USD" => [opt[1][1]*Notional, opt[2][1]*Notional ],
"Spot Premium USD" => [opt2[1][1]*Notional ,opt2[2][1]*Notional ],
"Fwd Delta" => [opt[1][2]*100 , opt[2][2]*100 ], "Spot Delta" => [opt[1][3]*100, opt[2][3]*100] )
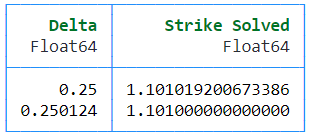
La salida coincide exactamente con Bloomberg:
![enter image description here]()
Usando el delta spot calculado de 25.0124 se obtiene el strike (1.101) de tu corredor:
DataFrame("Delta" => [, opt[1][3]], "Strike Solved" => [k_25D, f*exp((1/2)*^2*days_to_expiry/365 - ppf(opt[1][3]*exp(r1_cont *days_to_expiry/365))**sqrt(days_to_expiry/365))])
![]()
Personalmente, sospecho que aquí están ocurriendo dos cosas:
- El uso de Sticky Delta es bastante común en FX
- Solo pagaste un ligero "recargo" al precio justo, dados los datos de entrada (por ejemplo, redondeado al nearest 100)
¿Qué es Sticky Delta?
- Sticky Strike es realmente solo el Delta de Black Scholes calculado con Diferencias Finitas.
- Sticky Delta se refiere a ajustar la IV cuando subes y bajas (porque la IV está pegada al delta/moneyness).
Por lo tanto, hay 3 resultados posibles en relación con el Delta de Black Scholes:
- una IV que disminuye -> Sticky Delta será menor
- una IV plana -> Sticky Delta será idéntico
- una IV que aumenta -> Sticky Delta será mayor
Ahora, Bloomberg muestra convenientemente también el Sticky Delta. Como puedes ver, el delta pegajoso de hecho muestra 25D.
![enter image description here]()
PD. Si incluyeras la prima, no podrías usar una solución de forma cerrada y necesitarías resolver el strike numéricamente, por ejemplo, utilizando el método de búsqueda de raíces de Brent como sugieren Wystup y Reiswich.