Cálculos de VIX/¿Qué producto?

Question

Si el VIX spot es la volatilidad implícita de las opciones sobre el índice SPX. ¿Pero qué producto negociable sería ese? ¿No se pueden comprar técnicamente solo ETF que sigan al SPX (SPY) o comprar los futuros ES? El índice VIX spot se calcula a partir de los futuros del S&P500 o de los ETF?

Segundo, si el spot se basa en el efectivo SPX. ¿Cuál sería la volatilidad implícita para las opciones sobre los futuros del S&P a 3 meses? ¿Sería la misma que la de los contratos de futuros VIX a 3 meses? ¿Cuál es la relación entre la volatilidad implícita en los contratos de futuros del SPX y los futuros del VIX para el mismo período de tiempo? ¿No serían exactamente iguales?

Answer 1

El índice VIX se basa en opciones de compra y venta cercanas al vencimiento en el índice S&P 500. Las opciones de compra y venta hacen referencia al índice ('SPX') como subyacente y se negocian en el CBOE. Tenga en cuenta que cualquier opción o futuro que haga referencia al índice VIX se liquida en efectivo. Además, para fines de replicación y cobertura, es importante que VIX sea básicamente nada más que la volatilidad de un intercambio de varianza y debido a la naturaleza de este hecho, VIX puede ser básicamente cubierto estáticamente en las opciones de compra y venta subyacentes.

En resumen, el producto negociable son opciones de compra y venta cercanas al vencimiento en el índice S&P 500 y puedes replicar estáticamente el índice VIX negociando en las opciones de compra y venta, de manera similar a la construcción de un intercambio de varianza (aunque como se señaló anteriormente, VIX es la volatilidad de un intercambio de varianza no el valor del intercambio de varianza en sí). Las opciones, a su vez, se basan en el índice S&P 500

Aquí hay algunas referencias:

Hoja de Producto Vix por CBOE

Cálculo del Índice Vix

Especificaciones de Contrato de Opción del Índice S&P500

Answer 2

La respuesta de @Matt Wolf es muy acertada. Sin embargo, a veces una representación gráfica ayuda mucho en mi opinión a entender las cosas. Recientemente intenté responder una pregunta sobre swaps de varianza. Modifiqué el código ligeramente para visualizar lo que significa calcular el fair variance swap strike.

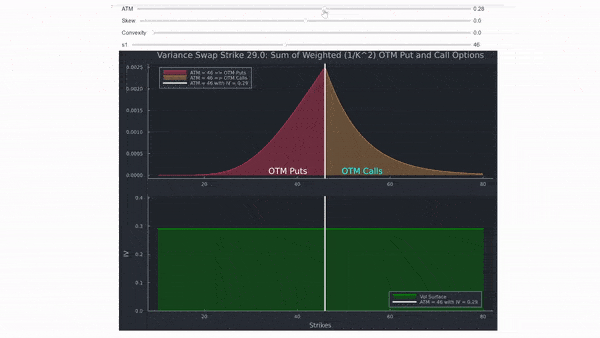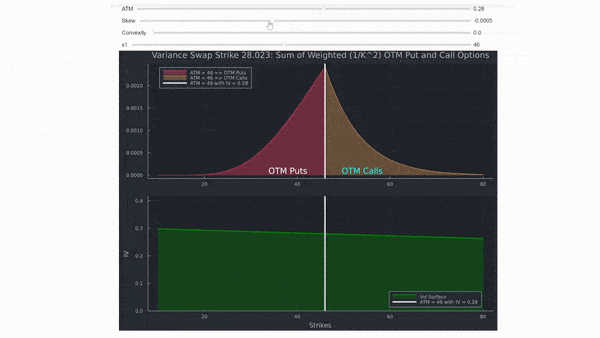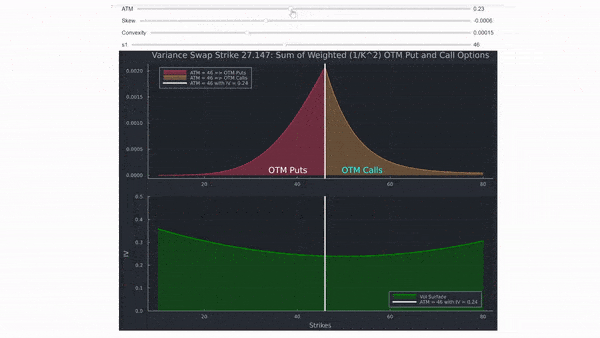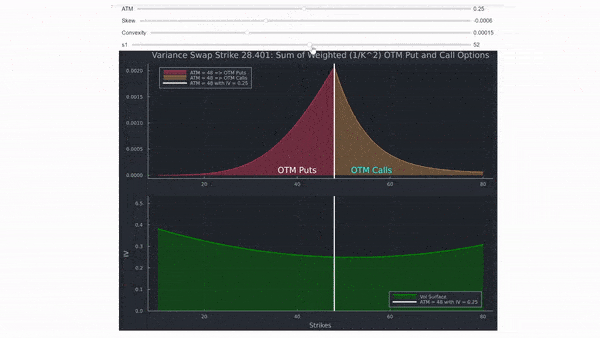
La siguiente captura de pantalla (y el GIF a continuación) trazan una superficie de volatilidad ficticia en la parte inferior, y calculan el fair variance swap strike como la integral de los precios ponderados de opciones fuera del dinero en todos los strikes. Es simplemente la función de los precios ponderados de put y call en diferentes strikes y fácil de seguir gráficamente (el área roja y naranja):

El índice VIX es esencialmente idéntico al gráfico anterior, que tiene la raíz cuadrada del fair variance swap strike calculado mediante integración. Uno podría verse tentado a pensar que este número de volatilidad es simplemente la tasa par de un swap de volatilidad pero un swap de volatilidad requeriría un ajuste de convexidad debido a la desigualdad de Jensen.

La intuición detrás de un Var swap es que un trader de opciones 'vanilla', siguiendo una estrategia de delta-hedging, esencialmente está replicando la ganancia de un swap de varianza ponderado donde los retornos al cuadrado diarios están ponderados por el gamma en dólares de la opción, que es más alto cerca del strike. Siguiendo este argumento un paso más adelante, un fair variance swap se puede demostrar que es igual a la integral de los precios ponderados de opciones fuera del dinero en todos los strikes. Por lo tanto, la tasa par (o el fair variance swap strike) se define como:

$$K_{var} = \frac{2}{B(0,T)T} \left[ \int_0^{F(0,T)} \frac{P(K,T)}{K^2} dK + \int_{F(0,T)}^\infty \frac{C(K,T)}{K^2} dK \right]$$ donde $T$ es la fecha de vencimiento del contrato, $B(0,T)$ el factor de descuento, $P(K,T)$ y $C(K,T)$ los precios de opciones europeas con strike $K$ y vencimiento $T$ y $F(0,T)$ el precio forward.

Estos pesos son inversamente proporcionales a los strikes al cuadrado ($1/K^2$), una aplicación de la fórmula en forma cerrada de Black Scholes para gamma, que asegura resultados en un gamma en dólares constante como se muestra a continuación.

Hay dos documentos de JP Morgan Variance Swaps y Just what you need to know about Variance Swaps que contienen la captura de pantalla, las fórmulas y muchos detalles, siendo este último más conciso. Personalmente, me gusta mucho Towards a Theory of Volatility Trading de Peter Carr y otros.

Cálculo del VIX

Ahora, no tienes un continuo de strikes disponibles, por lo que se calcula el VIX usando valores discretos. El documento técnico es muy claro e incluso replica todo el cálculo del VIX paso a paso (sólo se ignoran detalles menores como obtener el df correcto).

Específicamente, cada strike que entra en el cálculo (hay un filtrado que incluye solo opciones que tienen un precio de oferta distinto de cero y similares, los detalles exactos se describen en Metodología Matemática del Cboe Volatility Index®), se calcula como $$\frac{delta_K}{k^2} * df * Q(K_{i})$$ .

• $_ = \frac{_{+1} _{1}}{2}$ es la mitad de la diferencia entre los precios de strike adyacentes a ambos lados del strike
• $k^2$ es el strike al cuadrado
• $df$ es el factor de descuento (calculado con precisión en minutos de expiración a partir de la curva de rendimiento de tasa de interés a vencimiento constante con interpolación spline cúbica para obtener los rendimientos en las fechas de vencimiento)
• $Q(K_{i})$ es el mid de la oferta y la demanda de las opciones en ese k (solo se utilizan llamadas y puts OTM, excepto para ATM, que utiliza el promedio de llamadas y puts).

La suma de todos esos valores para todos los strikes (que cumplen los criterios de filtrado) para el plazo próximo (inferior a 30 días) y el siguiente plazo (superior a 30 días) se combina en un promedio ponderado a 30 días. Las reglas de filtrado hacen que el cálculo sea bastante tedioso si quieres replicarlo por completo.

Ejemplo gráfico

Sin embargo, podemos hacer nuestra vida mucho más fácil asumiendo que tenemos un continuo de strikes disponibles. Como se mencionó, expresaré el strike de varianza como $\sqrt{K_{var}}\times 100$ para ser consistente con el índice VIX. Además, asumo que los dividendos y las tasas de interés son cero para omitir el descuento y simplificar un poco la fórmula porque ATMS = ATMF.

• Los detalles y el código Julia utilizados a continuación se pueden encontrar en esta respuesta. Para el propósito de esta respuesta, solo recuerda que el VIX es el área debajo de las opciones OTM ponderadas (Puts rojo / Calls naranja).
• Según Black Scholes, la IVOL es conocida y constante. Este es el punto de partida del GIF a continuación (IVOL es una línea horizontal plana).
• La superficie de volatilidad existe principalmente porque hay colas gordas, asimetría, heterocedasticidad, saltos (crash), y demás. Ninguno de estos fenómenos del mundo real están representados en la fórmula de Black Scholes. El mercado simplemente desarrolló formas de tener en cuenta muchas de las deficiencias de Black Scholes. Puedes leer muchos más detalles aquí.
• Agregar asimetría (la línea se inclina hacia un lado) o agregar curtosis (la curva se dobla hacia arriba), no solo ajusta la deficiencia en Black Scholes, sino que también ajusta el VIX (Fair Var Swap strike, mostrado en el título del gráfico). Por lo general, el VIX es más alto, en relación al ATM, cuanto más pronunciada sea la asimetría y la curtosis. Por eso, la IVOL de 1M ATM para SPX suele ser más baja en comparación con el VIX.

Haciendo el gráfico interactivo se muestra cómo el VIX (y Var Swap) dependen del nivel, así como de la forma de la superficie de volatilidad (desafortunadamente imgur no permite un tamaño mayor, por lo tanto una mejor resolución).