Bienes públicos sobre el costo de la reducción de emisiones

Question

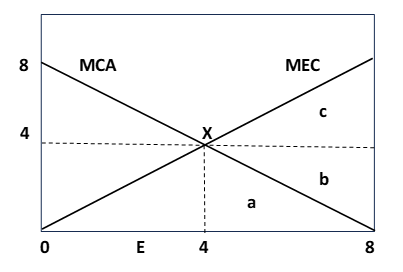
Hay un fabricante y una pesquería. Sea $E$ el efluente del fabricante. El costo marginal de abatimiento soportado por el fabricante es $M C A=8-E$. El costo marginal externo soportado por la pesquería es $M E C=E$. Suponga que el fabricante tiene el derecho de liberar efluente sujeto a control gubernamental. (a) ¿Cuál es el nivel de contaminación eficiente? (b) ¿Cómo se puede usar una tarifa de efluente para lograr el nivel de contaminación eficiente? (c) ¿Cómo puede usarse la negociación entre las dos partes para lograr el nivel de contaminación eficiente?

(a) El nivel eficiente de contaminación satisface $M C A=8-E=E=M E C$, lo que da $E=4$

(b) Supongamos que la tarifa de efluente es $F$ por unidad de contaminación. El fabricante elegiría las emisiones para satisfacer $M C A=8-E=F$, lo que da $E=8-F$. Por lo tanto, una tarifa de efluente de $F=4$ induciría el nivel de contaminación eficiente $E=4$.

(c) El aumento en el costo total de abatimiento de $E=8$ a $E=4$ es $T C A=$ $\frac{1}{2} \cdot 4 \cdot 4=8$. La disminución en el costo externo total de $E=8$ a $E=4$ es TEC $=4 \cdot 4+\frac{1}{2} \cdot 4 \cdot 4=24$. Por lo tanto, la pesquería podría ofrecer al fabricante un pago entre 8 y 24 para reducir el efluente de 8 a 4 .

Pregunta: No entiendo la solución de (c). ¿Alguien puede ayudarme a explicar la parte (c)?

Answer 1

Encontrar TCA y TEC son ejemplos del requisito común en economía de calcular una cantidad total cuando se conoce la cantidad marginal correspondiente. Matemáticamente, esto es equivalente a encontrar el área debajo de la curva que representa la cantidad marginal. A veces esto requiere cálculo integral, pero cuando, como aquí, las curvas marginales son lineales, es más simple usar las fórmulas para el área de un triángulo y un rectángulo.

El diagrama abajo traza tanto MCA como MEC contra E. El punto X, su intersección, corresponde al nivel de contaminación eficiente.

El cambio en efluente requerido para alcanzar el nivel eficiente va desde $E=8$ hasta $E=4$, por lo que estamos interesados en las áreas del lado derecho del diagrama. Así que el cambio en $TCA$ es el triángulo a cuya área (1/2 x base x altura) es $\frac{1}{2} \cdot 4 \cdot 4=8$. Para el cambio en $TEC$ necesitamos el rectángulo que consiste en los triángulos a y b (base x altura) que es $4 \cdot 4 = 16$ y también el triángulo c cuya área es $\frac{1}{2} \cdot 4 \cdot 4=8$ haciendo un total de $16+8=24$.