Complemento perfecto preferencias en una economía de intercambio

Question

Así que tengo un examen en un rato, entiendo que para encontrar la elección óptima tienes que igualar la tangente de las dos curvas de indiferencia. Sin embargo, si la otra curva de indiferencia es un complemento perfecto, ¿cuál es la MRS? Calculé la MRS como infinito/infinio.

Echa un vistazo a la pregunta a continuación:

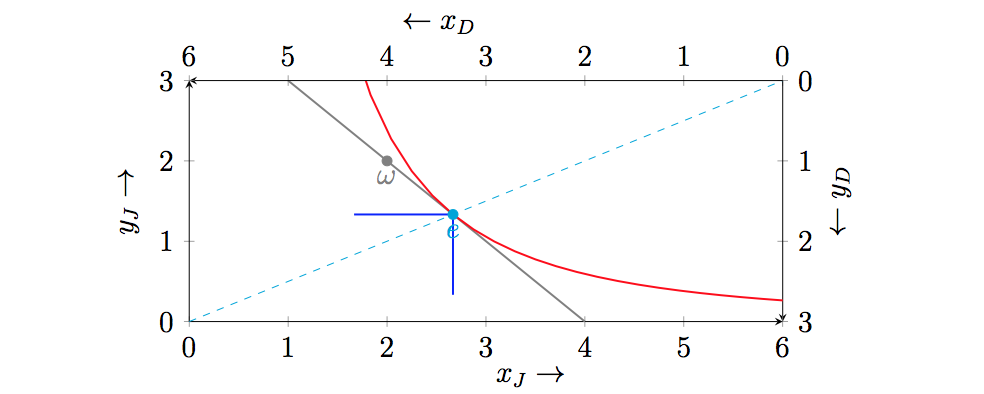
Supongamos que Jane tiene una dotación de 2 unidades de x y 2 unidades de y, y tiene preferencias dadas por la función de utilidad $u_J(x_J, y_J) = x_J^{2/3} \cdot y_J^{1/3}$. Supongamos que Derek tiene una dotación de 4 unidades de x y 1 unidad de y, y tiene preferencias dadas por la función de utilidad $u_D(x_D, y_D) = \min(x_D, 2 y_D)$.

1. En un diagrama de caja de Edgeworth, indica el conjunto de asignaciones eficientes de Pareto. Explica cómo se determina.
2. Calcula el equilibrio competitivo (precios y cantidades) para la economía de intercambio

¿Estaba en lo correcto acerca de la MRS siendo infinito sobre infinito? Si es así, ¿cómo calcularía el resultado Pareto Eficiente cuando no puedo igualar las MRS? Estaba pensando que la solución estaría en uno de los vértices de la curva de indiferencia de Derek pero no estoy seguro (porque los puntos no son dif).

¿Alguna idea?

Answer 1

El conjunto de asignaciones eficientes de Pareto consta de asignaciones factibles $((x_J, y_J), (x_D, y_D))$ que satisfacen $y_J=\displaystyle\frac{x_J}{2}$.

El Equilibrio Competitivo es el precio $(p_x, p_y=1)$ que satisface las siguientes condiciones:

• Requisito de presupuesto: $p_xx_J+ y_J = 2p_x + 2$ y $p_xx_D+ y_D = 4p_x + 1$
• Condiciones de equilibrio: $\displaystyle\frac{2y_J}{x_J} = p_x$ y $y_D=\displaystyle\frac{x_D}{2}$

Resolviendo el sistema de ecuaciones obtenemos el vector de precios de equilibrio como: $(p_x, p_y) = (1,1)$ y la asignación de equilibrio es $((x_J, y_J), (x_D, y_D)) = \displaystyle \left(\left(\frac{8}{3}, \frac{4}{3}\right), \left(\frac{10}{3}, \frac{5}{3}\right)\right)$

Answer 2

Los complementos perfectos son equivalentes a la utilidad de Leontief:

$U(x,y) = min(x/a_x, y/a_y)$

La TMS se define como:

$MRS_x,y = MU_x / MU_y$

Dado que esta función de utilidad no es diferenciable, el concepto de sustitución marginal no está bien definido para Derek. Sin embargo, no necesitamos argumentos marginales para que Derek resuelva el problema. Una función no tiene que ser diferenciable para tener un máximo único. Derek tiene preferencias de Leontief y por lo tanto quiere consumir $x_d = 2 y_d$ para todos los precios. Él agota su riqueza (su dotación): $4 p_x + 1 p_y = w = x_d p_x + y_d p_y$

Podemos usar esto para resolver $y_d = (4 p_x + 1 p_y) / (p_y + 2 p_x)$ (eqn 1) y $x_d = 2 (4 p_x + 1 p_y) / (p_y + 2 p_x)$ (eqn 2).

Jane tiene preferencias Cobb-Douglas y por lo tanto quiere gastar una parte constante del presupuesto en x: $x_j p_x / (2 p_x + 2 p_y) = 2/3$ y $y_j p_y / (2 p_x + 2p_y) = 1/3$. También podemos resolver esto para $x_j = (2/3) / (p_x / (2 p_x + 2 p_y) )$ (eqn 3) y $y_j = (1/3) / (p_y / (2 p_x + 2p_y))$ (eqn 4).

Sin embargo, también sabemos que en equilibrio $y_j + y_d = 3$ (eqn 5) y $x_j + x_d = 6$ (eqn 6). Esto son 6 ecuaciones y 6 incógnitas ($p_x, p_y, x_d, y_d, x_j, y_j$) y se pueden resolver para los precios de equilibrio y la asignación.