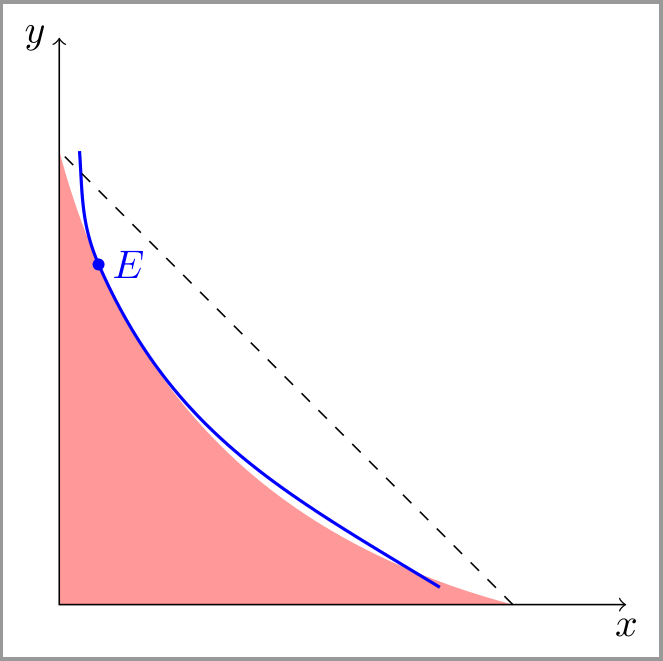
La convexidad puede ser una suposición muy importante ya que gran parte del análisis económico se basa en trabajar con conjuntos convexos, lo que facilita las cosas.
Es muy importante destacar que la convexidad de los conjuntos nos permite trabajar con los teoremas del Hiperplano Separador y el Hiperplano Soporte, los cuales tienen aplicaciones en muchos resultados en economía, como se discute parcialmente aquí y aquí.
Aquí también hay un ejemplo breve y concreto de algo para lo que necesitamos la convexidad del conjunto de presupuesto:
Supongamos que deseas demostrar que la Demanda Marshalliana $x(p,m)$ es de un solo valor para cada combinación de precio ($p$) e ingreso (no negativo) ($m$). Es decir, existe una Función de Demanda Marshalliana, ya que sin el valor único tendríamos una Correspondencia de Demanda Marshalliana (es decir, tendríamos múltiples combinaciones de bienes como parte de la elección de demanda óptima para un único precio y nivel de ingreso), lo cual puede ser más complicado de trabajar. Este es un resultado bastante útil con el que (casi) siempre trabajamos en textos de pregrado. Para eso necesitas preferencias estrictamente convexas y un conjunto de presupuesto convexo $B(p,m)$. La demostración es la siguiente:
Si dos puntos $x_1$ y $x_2$ son ambos elementos de la demanda $x(p,m)$ con precios dados $p$ e ingreso $m$, es decir, si $x_1, x_2 \in x(p,m)$, entonces por definición debe existir indiferencia entre los dos puntos, es decir, $x_1 \sim x_2$. Para una función de demanda de valor único, dos puntos diferentes $x_1$ y $x_2$ no pueden existir para un único nivel dado de precios e ingresos, es decir, tendrían que ser el mismo punto. En otras palabras, $x_1 = x_2$. Lo probamos por contradicción. Supongamos que $x_1 \neq x_2$.
Para todo $\lambda \in (0,1)$, tenemos que $\lambda *x_1 + (1-\lambda) *x_2 \in B(p,m)$ por la convexidad de $B$. Por la estricta convexidad de las preferencias, tenemos que $\lambda *x_1 + (1-\lambda) *x_2 \succ x_1$. Sin embargo, esto contradice el hecho de que $x_1 \in x(p,m)$ en primer lugar. Por lo tanto, $x_1 = x_2$.
Entonces, en palabras, alguna combinación de $x_1$ y $x_2$ es mejor que solo $x_1$ en el precio y nivel de ingreso dados. Pero tal combinación también es alcanzable en ese precio y nivel de ingreso debido a la convexidad del conjunto de presupuesto. Aquí es donde es importante la suposición de convexidad del conjunto de presupuesto. Además, si para un precio y nivel de ingreso dado hay un punto (en este caso una combinación de $x_1$ y $x_2$) que es estrictamente mejor y alcanzable, entonces esto contradice el punto de partida original de que $x_1$ es un punto en la función de demanda para el precio y nivel de ingreso dado.
Como nota al margen, creo que es un poco confuso hablar de productores en tu publicación cuando se trata de restricciones presupuestarias. Si estamos viendo una restricción presupuestaria, deberíamos estar discutiendo sobre los consumidores.