A menos que me esté perdiendo lo obvio, ¡no veo la pregunta respondida? En mi opinión, tratar de entender en lenguaje simple qué $\alpha, \beta, \rho$ significan requiere una explicación de qué hacen estos parámetros y por qué es útil.
Aquí está mi intento: Black (todas las fórmulas de Black Scholes) asume(n) que la Volatilidad Implícita es independiente de la huelga (constante y conocida). Sin embargo, este suele no ser el caso y si grafica (cotizada) IVOL y huelga, se ve lo que se llama una sonrisa o inclinación. SABR se puede utilizar para interpolarnos una sonrisa de volatilidad.
Antes de hablar sobre SABR, consideremos $\beta$ por separado. El modelo CEV no asume un proceso lognormal (Black) sino que es más general: $$dF = \alpha * F ^ \beta * dW$$ donde $\alpha$ corresponde a la volatilidad CEV (establece el nivel general de volatilidad), $\beta$ es el parámetro CEV (que determina el sesgo) y $W$ es el movimiento Browniano.
Ahora, en términos de lo que el nivel, sesgo y sonrisa en realidad significan o cómo lucen, recomiendo echar un vistazo a esta ilustración en el mercado de divisas. El nivel será lo que se muestra como la volatilidad plana para todas las huelgas (solo ATM simple), el sesgo es el parámetro CEV. Para $\beta < 1$, la sonrisa de volatilidad es una función decreciente del precio de huelga. Un problema importante es que no es capaz de producir una sonrisa (las alas con pendiente ascendente en el ejemplo de FX que enlacé).
Ahí es donde entra SABR: Además de CEV, la nueva suposición es que la volatilidad no es constante como en CEV sino un proceso estocástico en sí. Por lo tanto, $\sigma$ misma está gobernada por una EDP, al igual que la tasa forward (como se asume en Black y CEV). Los dos movimientos Brownianos (para tasa forward y volatilidad) están correlacionados a través del coeficiente de correlación $\rho$.
Cómo obtener o establecer $\beta$ se explica aquí. Esta respuesta muestra cómo se puede estimar $\beta$ y cuál es el efecto e interpretación de $\beta$.
Una vez que tenga $\beta$,
- $\alpha$ controla principalmente la altura general (como en CEV),
- $\rho$ (correlación) controla el sesgo (para beta establecido) y
- $\nu$ (volatilidad de volatilidad) controla la sonrisa (no parte de la pregunta pero crucial) .
El gif a continuación utiliza Julia y las fórmulas a partir de 2.17 en adelante, comenzando en P.89, de Managing Smile Risk. Wilmott, 1, 84-108,.
# cargar paquetes
using Plots, PlotThemes, Interact, LaTeXStrings
theme(:juno)
#definir entradas
, , , , t_ex, f1, f2, f3, t_ex = 1, 0.05, 0, 1, 1, 0.03, 0.05, 0.07, 1
K = 0.01:0.0001:0.1
#definir la expresión
function _b(,, , , t_ex, f, K)
A = /(((f*K)^((1-)/2))*(1+((1-)^2)/24*log(2,(f/K))+ ((1-)^4)/1920*log(4,(f/K))))
B = 1+(((1-)^2)/24*(^2/(f*K)^(1-))+(1/4)****/((f*K)^((1-)/2))+(2-3*^2)/24*^2)*t_ex
z = /*(f*K)^((1-)/2)*log(f/K)
_z = log((sqrt(1-2**z+z^2)+z-)/(1-))
atm = /(f^(1-))*(1+(((1-)^2)/24*(^2/(f*K)^(1-))+(1/4)****/((f*K)^((1-)/2))+(2-3*^2)/24*^2)*t_ex)
cond = f==K
return cond ? atm : A*z/_z*B, atm
end
# definir gráficos
plot(K,[x[1] for x in _b.(,, , , t_ex, f, K)], size =(800,500), margin=5Plots.mm,
title = "Modelo SABR \n( = $, = $, = $, = $, "L"$ t_{ex}"*" = $t_ex)",
label = "f = $(round((f*100),digits=1))%",
xlabel = "Huelgas",
ylabel = "Volatilidad")
ylims!((0, ylims()[2]+ylims()[1]))
vline!([f], label = "Vol ATM = $(round(minimum([x[2] for x in _b.(,, , , t_ex, f, K)]),digits = 2))")
ylims!((0,maximum(x[1] for x in _b.(,, , , t_ex, f3, K))))
xlims!((minimum(K),maximum(K)))
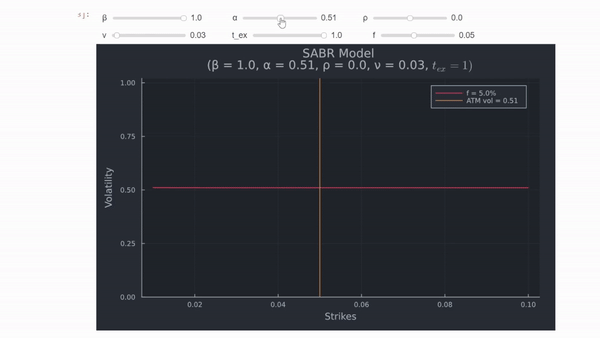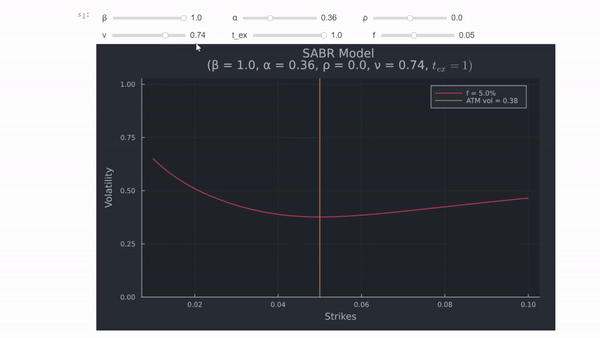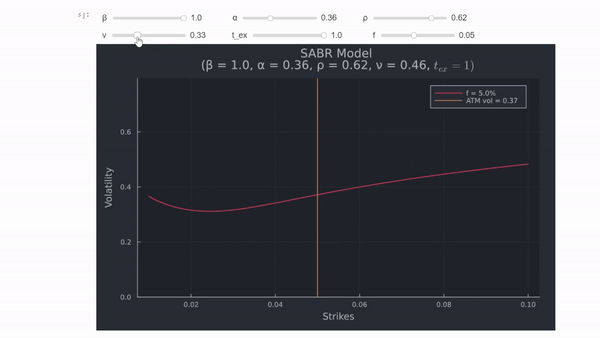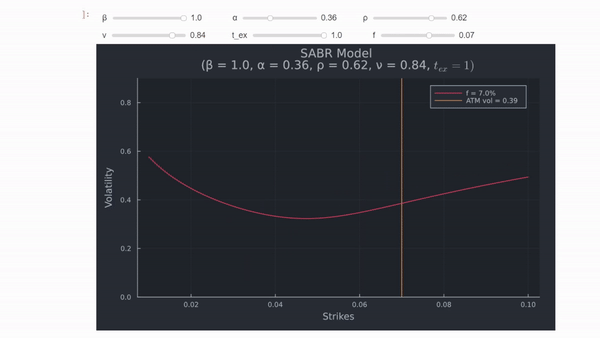
![entrar descripción de la imagen aquí]()
Agregando unas líneas similares a esta respuesta hace que el gráfico sea interactivo.
![entrar descripción de la imagen aquí]()
Cambiar el nivel de correlación hace que la sonrisa "gire" alrededor del punto ATM, y si $\rho < 0$, la volatilidad es menor para precios de huelga más altos (ITM) y viceversa (la volatilidad aumenta en el lado izquierdo de la figura).
Por lo tanto, es posible ajustar toda la curva de volatilidad con este modelo. Un comentario adicional, NO ajustará las vols citadas ya que es el mejor ajuste general alrededor de todos los puntos. Si el ajuste de vols citadas es una característica deseada, se podría por ejemplo combinar de forma lineal por tramos dentro del espectro citado y SABR para extrapolación.
Editar:
Seguí la notación en la P.13 del documento original que establece que
Los tres parámetros , y tienen diferentes efectos en la curva: el parámetro controla principalmente la altura general de la curva, al cambiar la correlación se controla la inclinación de la curva, y al cambiar la vol de vol se controla cuánta sonrisa exhibe la curva.
La otra respuesta (por cierto, al referirse a la respuesta anterior a la mía es confuso porque se pueden ordenar las respuestas de varias maneras) usa la notación de Wikipedia al parecer. Wikipedia define como $\sigma$ y como , lo cual es bastante confuso, dada la elección de parámetros en el documento original. Además, los autores (vea el documento en la P.8) eligieron el nombre "modelo estocástico", que se ha conocido como el modelo SABR porque hacen que (la volatilidad) sea un proceso estocástico. Eso también es algo que la otra respuesta claramente parece haber pasado por alto.




5 votos
¿Al menos investigaste en Google? Hay mucho material disponible en línea sobre este modelo.
0 votos
Sí, después de una larga búsqueda solo pregunté. No soy una persona de matemáticas, así que estoy tratando de entender en un lenguaje sencillo su importancia sin fórmulas complejas.