Me encontré con una presentación en la que se afirma que utilizando un modelo de volatilidad local el PnL de una opción es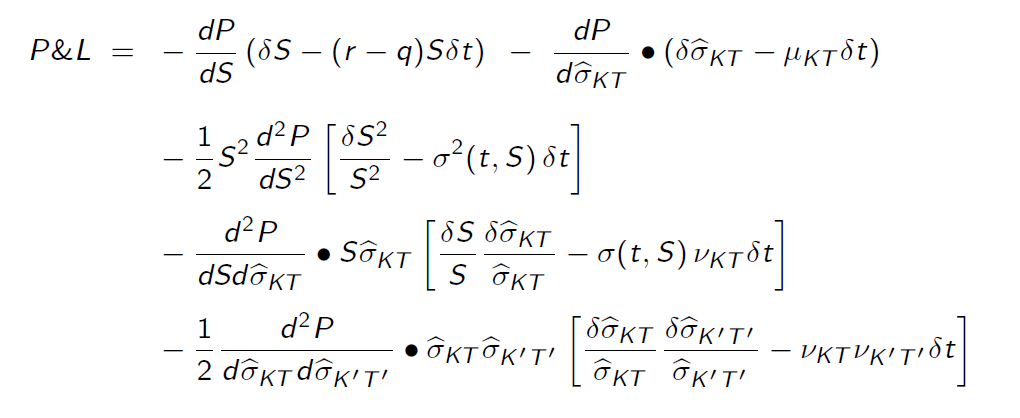 
y 
¿Qué quiere decir con spot/vol correl = -100%?
Respuesta
¿Demasiados anuncios?
El modelo LV es un tipo particular de modelo en el que la volatilidad implícita de una opción vanilla europea de una huelga y vencimiento dados emerge como una función determinística del tiempo, nivel spot y la función de volatilidad local utilizada $\sigma(\cdot, \cdot)$. $$ \hat{\sigma}_{KT} = f(t, S_t; \sigma) $$ de manera que utilizando Itô se puede escribir \begin{align} \frac{ dS_t }{S_t } &= \mu dt + \sigma(t,S_t) dW_t^\Bbb{Q} \\ d\hat{\sigma}_{KT} &= \left( \frac{\partial f}{\partial t} + \frac{\partial f}{\partial S} (r-q) S_t + \frac{1}{2} \frac{\partial^2 f}{\partial S^2} \sigma^2(t,S_t) S_t^2 \right) dt + \frac{\partial f}{\partial S} \sigma(t,S_t) S_t dW_t^\Bbb{Q} \\ &:= \mu_{KT} dt + \nu_{KT} \hat{\sigma}_{KT} dW_t^\Bbb{Q} \end{align} de donde se ve que si el mercado se comporta como postulado por el modelo $$ \Bbb{E}\left[ \frac{\delta S}{S} \frac{\delta \hat{\sigma}_{KT}}{\hat{\sigma}_{KT}} \right] = \sigma(t,S_t) \nu_{TK} \delta t$$ y el término Volga en la ecuación de P&L anterior desaparece en expectativa, independientemente del instrumento considerado, como se requiere de un modelo de mercado genuino (niveles de equilibrio sin dependencia del payoff).
Ahora, observando la correlación entre spot/volatilidad implícita que se cotiza en el modelo de volatilidad local tenemos: $$ \frac{d \langle \ln S, \hat{\sigma}_{KT} \rangle_t}{\sqrt{ d \langle \ln S \rangle_t d \langle \hat{\sigma}_{KT} \rangle_t } } = \frac{ \sigma^2(t,S_t) S_t \frac{\partial f}{\partial S} dt }{ \sigma^2(t,S_t) S_t \left\vert \frac{\partial f}{\partial S} \right\vert dt } = \text{sign}\left(\frac{\partial f}{\partial S}\right) = \text{sign}\left( \frac{{\partial \hat\sigma}_{KT}}{\partial \ln S} \right) $$ debido a que $S_t \geq 0, \forall t>0$
En otras palabras, la correlación es del +100% o -100% o 0% dependiendo del signo del término en el RHS.
Resulta que la última derivada parcial es negativa para los mercados de opciones vanilla con sesgo negativo, que es el caso de (la mayoría de) los mercados de renta variable. Para tener una mejor comprensión de este resultado que requeriría una respuesta separada, consulte el libro de Bergomi, capítulo 2, ecuaciones (2.58)-(2.59)-(2.60).
