Convexidad de la Función de Demanda del Mercado

Question

La función de demanda del mercado puede ser tanto cóncava como convexa. Estoy buscando condiciones bajo las cuales se pueda considerar como convexa una función de demanda general del mercado. ¿Por ejemplo, preferencias convexas o una función de utilidad cóncava implicarían una curva de demanda de mercado convexa?

No estoy preguntando por el conjunto de demanda, sino más bien por la función.

Me cuesta imaginar una función de demanda de mercado cóncava, pero la literatura a menudo tiene en cuenta esta posibilidad, lo que me lleva a creer que no se puede descartar sin imponer condiciones adicionales.

La razón por la que me cuesta imaginar funciones cóncavas es que cuando maximizamos con una función de utilidad estándar, lo que resultará con funciones típicas es algo como:

1. Cobb-Douglas: $X=(\alpha/(+)) M/2p$

2. Complementos perfectos (mín): $X=m/(p1 + p2)$

3. Sustitutos perfectos: $X=M/p$; donde X es la demanda de algún bien, M es el presupuesto, p el precio (del bien 1 o 2) y y son solo parámetros de utilidad.

que son todos convexos.

Además, dado que la demanda del mercado se define más a menudo como la suma de las demandas individuales (que anteriormente parecen ser principalmente convexas) y la suma de funciones convexas es en sí misma una función convexa, entonces la demanda del mercado debería ser, en su mayoría, una función convexa parece.

¿Se puede hacer una afirmación más general aquí sobre cuándo la curva de demanda del mercado es convexa?

Answer 1

Desde un punto de vista matemático, una función de la forma

$$Q_d = \left( \frac {A-p}{B}\right)^{1/\gamma},\;\; \gamma > 1$$

presentará una segunda derivada negativa y, por lo tanto, será estrictamente cóncava (para $\gamma =1$ obtenemos una función de demanda lineal). La función toca el eje (vertical) $p$ para $(Q_d=0,p=A)$, y el eje horizontal $Q$ para $(Q_d = (A/B)^{1/\gamma}, p=0$). Es decir, esto es "cóncavo todo el tiempo", no solo cóncavo en el medio que eventualmente se vuelve convexo. Típicamente, esperamos que $A>B$.

Invirtiendo, obtenemos

$$p=A-BQ_d^{\gamma}$$

Ahora bajemos al nivel individual, y asumamos preferencias cuasi-lineales en ingresos, una formulación apropiada cuando miramos un bien "contra todos los demás":

$$v(q,y) = u(q) + y,\;\;\; s.t. \;\;pq+y = M$$

Las condiciones de primer orden darán

$$u'(q) = \lambda p,\;\;\;\ \lambda =1$$

Combinando con la función de demanda inversa obtenemos

$$u'(q) = A-BQ_d^{\gamma}$$

donde $Q_d = \sum q$.

Integrando tenemos

$$\int u'(q) dq = A\int dq - B\int \left (\sum q\right)^{\gamma}dq$$

de lo cual llegamos a (ajustando las constantes arbitrarias de integración a cero)

$$u(q) = Aq-\frac{B}{1+\gamma}Q_d^{1+\gamma}$$

Obtuvimos este resultado asumiendo que el individuo cree que su propia demanda no afecta la demanda de otros individuos. Por lo tanto, tenemos una externalidad negativa: cuanto más "masivo" es un bien (cuanto más demandado), menos utilidad obtenemos de él (así que la demanda de cualquier individuo no afecta a la demanda de ningún otro individuo, pero su suma sí afecta a los elementos individuales). Entonces, esta especificación sería apropiada para bienes que no se caracterizan por el aspecto de la "seguridad del rebaño", sino que apelan a nuestra búsqueda de individualismo y singularidad personal.

Supongamos ahora que no queremos tener esta externalidad negativa en la utilidad individual. Entonces, asumimos que todos los consumidores son idénticos, y comenzamos con la especificación de utilidad,

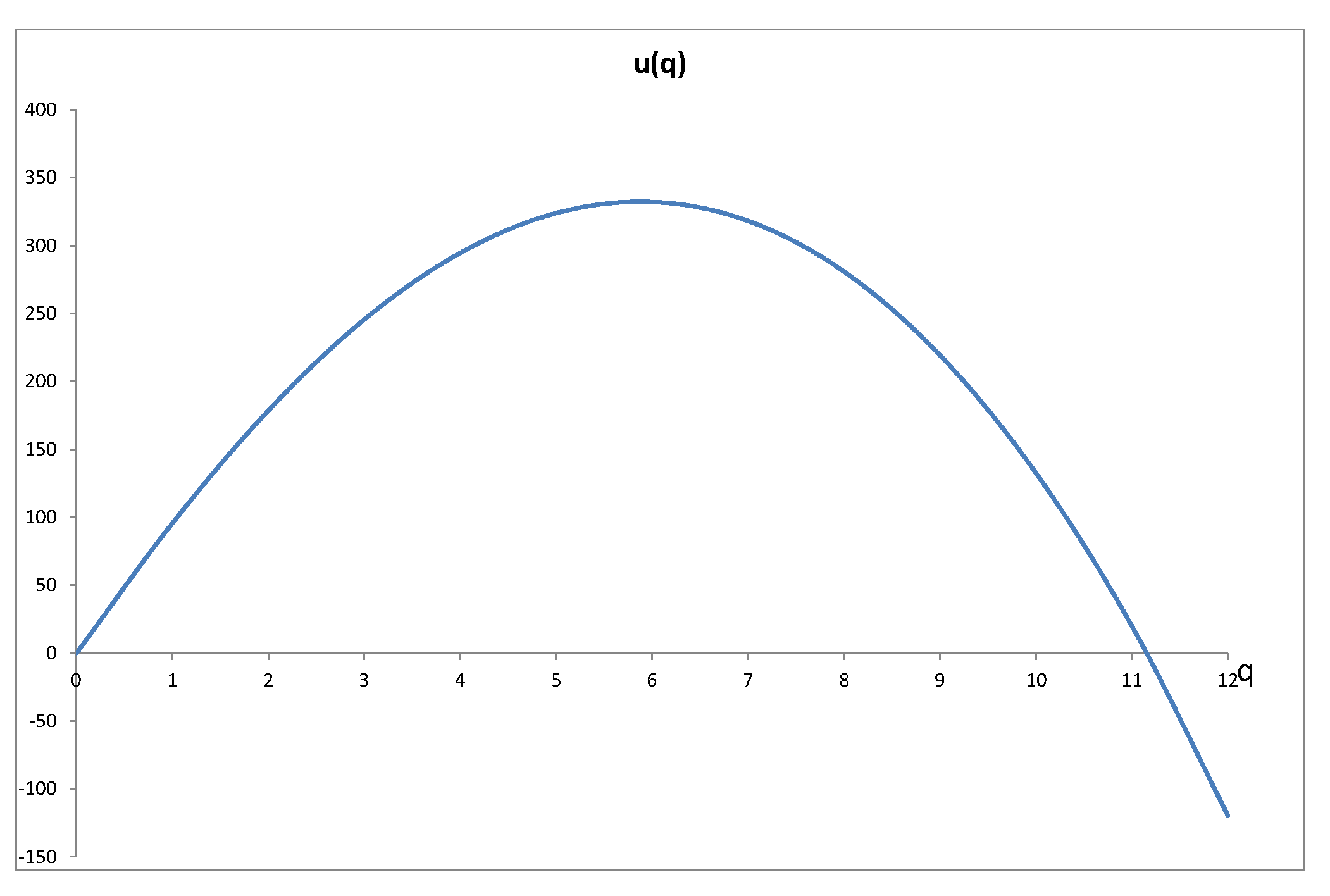
$$u(q) = aq-\frac{b}{1+\gamma}q^{1+\gamma}$$

Esta especificación de utilidad implica que existe un nivel de utilidad máximo del bien y luego la utilidad disminuye, por lo que pertenece a la familia general de preferencias "cuadráticas".

Indicativamente, para $a=100, b=10, \gamma=1.3$ tenemos

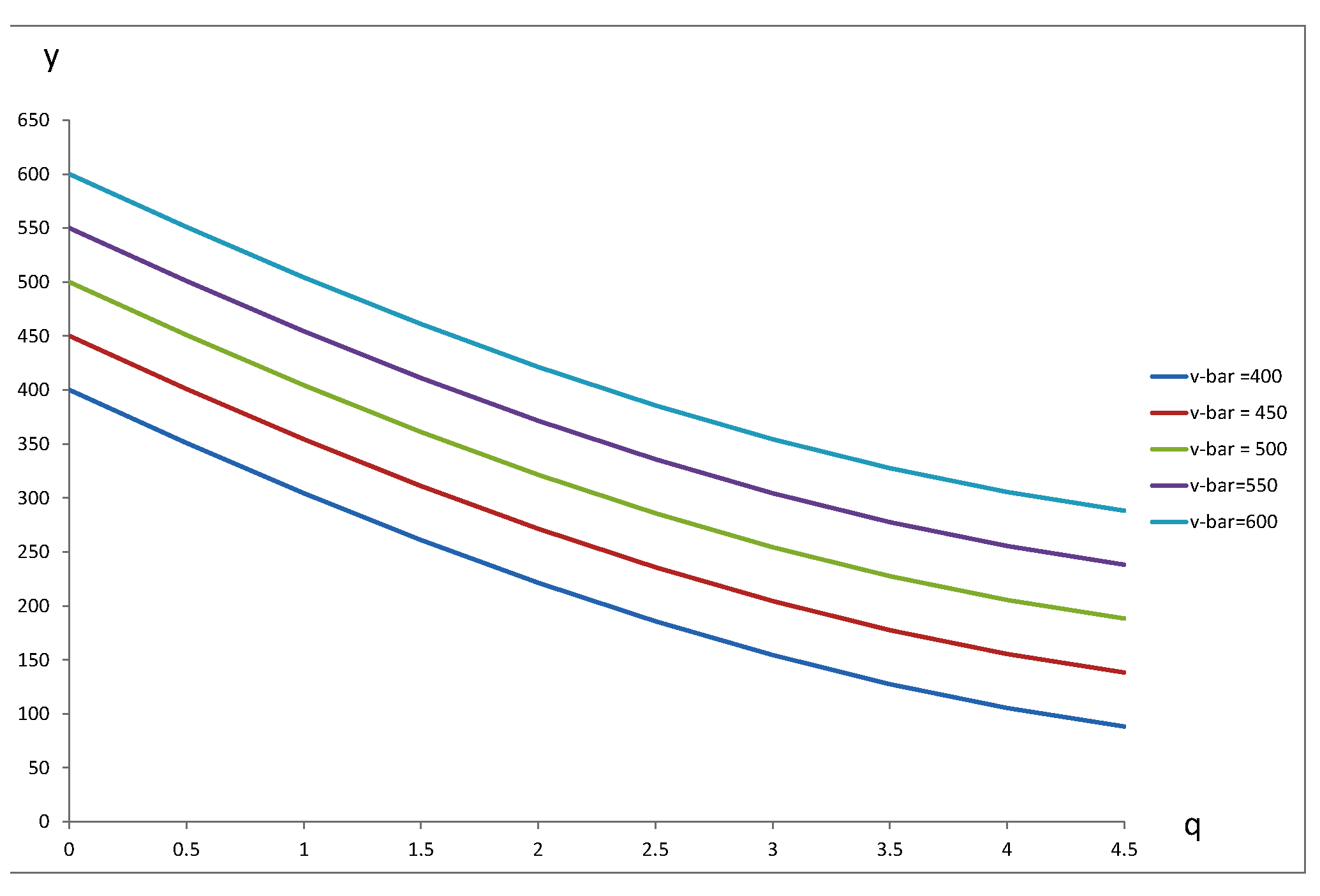
El mapa de indiferencia se construye calculando

$$y = \bar v - \left[aq-\frac{b}{1+\gamma}q^{1+\gamma}\right]$$

para valores arbitrarios de $\bar v$ (que, en preferencias cuasi-lineales, corresponden a la restricción de ingresos). Para $\bar v = M=400,450,500,550,600$ el mapa luce como

Tal especificación de utilidad individual dará la relación óptima

$$a - bq^{\gamma} = p$$

y la demanda individual

$$q = \left( \frac {a-p}{b}\right)^{1/\gamma}$$

Sumando sobre todos los $N$ consumidores obtenemos

$$Q_d = N\left( \frac {a-p}{b}\right)^{1/\gamma}$$

y queremos llegar a la función de demanda del mercado

$$Q_d = \left( \frac {A-p}{B}\right)^{1/\gamma}$$

Esto puede ocurrir si identificamos $A=a$ y $B = b/N^{\gamma}$.

Answer 2

Ten en cuenta que una función es convexa si y solo si multiplicando esa función por -1 resulta en una función cóncava.

Un ejemplo sería una suegra vengativa, que obtiene placer de la desgracia de su yerno. Sea x un resultado en la vida del pobre hombre, y $u(x)$ la felicidad que obtiene de x, que es cóncava. Deje que $-u(x)$ sea la función de utilidad de la suegra. Es convexa.

Answer 3

A nivel individual (y en el caso diferenciable), las derivadas de primer orden del sistema de demanda están relacionadas con las derivadas de segundo orden de la función de utilidad. Esto implica que las derivadas de segundo orden del sistema de demanda están relacionadas con las derivadas de tercer orden de la función de utilidad. \ De hecho, a partir de la condición de primer orden para la optimalidad: $$ \frac{\partial u}{\partial x }(x^F(p,\lambda)) = \lambda p, \\ $$ donde $x^F$ denota las demandas óptimas de Frisch o de constante $\lambda$. Manteniendo $\lambda$ constante, vemos que los cambios en el vector de precios $p$ afectan a las demandas óptimas de la siguiente manera: \begin{eqnarray*} \frac{\partial^2 u}{\partial x \partial x'}(x^F(p,\lambda))\frac{\partial x^F}{ \partial p'}(p,\lambda) = \lambda I_K \\ \Leftrightarrow \frac{\partial x^F}{ \partial p'}(p,\lambda) = \lambda \left[ \frac{\partial^2 u}{\partial x \partial x'}(x^F(p,\lambda)) \right]^{-1}. \end{eqnarray*} La última equivalencia requiere una matriz hessiana regular. Esta igualdad ilustra que un sistema de demanda cóncavo requiere restricciones en las derivadas de tercer orden de $u$. Una conclusión similar se aplica para el sistema de demanda de Marshall $x^M(p,m)$ (utilice la identidad de Roy para demostrar la afirmación).