No es tanto que estés calculando de forma errónea, sino que lo que estás calculando no tiene sentido en el contexto en el que estás intentando usarlo ("la tasa anual del préstamo"). Básicamente estás tratando de comparar manzanas con naranjas.
Has tomado el total de intereses pagados (durante uno o 20 años), lo has expresado como fracción del monto original del préstamo, y luego has "descompuesto" esa tasa para obtener un "porcentaje anual".
(Tus cifras son 4.84% por 1 año; 2.71% por 20 años. Como se señala a continuación, estas están "ligeramente equivocadas" porque (a) tomaste los intereses después de un mes adicional, y (b) deberías haber usado el número de meses, no años, en el proceso de descomposición. Mis cifras correspondientes son 4.38% y 2.67%.)
Luego la pregunta es: ¿qué representan estas tasas?
Son las tasas de retorno necesarias en un solo depósito único a plazo fijo (donde los intereses se capitalizan mensualmente) para ganar el equivalente de los intereses pagados en la hipoteca durante el mismo periodo.
-
Entonces, $165,000 depositados por un año a una tasa anual de 4.38%, donde los intereses se capitalizan mensualmente, crecerían en $7,373 después de un año.
-
De manera similar, $165,000 depositados por 20 años a una tasa anual de 2.67%, donde los intereses se capitalizan mensualmente, crecerían en $116,280 después de veinte años.
(Estas cifras también se aplicarían a una forma extrema de una "hipoteca globo" donde no se realizaran pagos durante el plazo del préstamo, y se devolviera toda la cantidad adeudada (intereses acumulados + capital original) como un único pago al final del periodo.)
Sí, el 2.67% es mucho más bajo que el 4.38%, pero esto solo muestra el efecto del interés compuesto a lo largo de un periodo más largo.
Utilizando la misma calculadora de pagos que tú1 y una calculadora de depósitos fijos que encontré2, preparé la siguiente tabla (que también muestra las cifras para el término completo de 30 años):
4.5% Préstamo liquidado después 1 Año 20 Años 30 Años
------- -------- --------
Meses: 12 240 360
Monto del préstamo: 165,000 165,000 165,000
Interés pagado (a): 7,370 116,315 135,971
Total pagado: 172,370 281,315 300,971
Interés como % del préstamo (b): 4.47% 70.49% 82.41%
Tasa efectiva anual (c): 4.38% 2.67% 2.01%
Retorno de inversión (d): 172,373 281,280 301,400
Notas:
(a) El interés pagado se obtiene de la página de la calculadora de préstamos, utilizando la línea de octubre de 20xx en cada caso. Nota: Originalmente transcribí mal la cifra de 1 año como 7,360 (dando tasas ligeramente diferentes %).
(b) Este es el interés dividido por el monto del préstamo y expresado como un porcentaje.
(c) Esta es la cifra de (b) convertida a una tasa efectiva anual, utilizando
( ( 1 + interés/préstamo ) ^ ( 1 / meses ) - 1 ) * 12
Esto es similar al cálculo que hiciste para obtener 2.71%, excepto (i) que uso el número de meses al tomar la raíz enésima, y luego multiplico por 12; y (ii) utilizo las cifras de octubre donde tú usaste las cifras de diciembre.
(d) Estas cifras son de la calculadora de depósitos fijos, utilizando la tasa mostrada en la línea anterior (por ej. "2.67"). Si se utiliza la TAE exacta calculada, las cifras de la calculadora coinciden al dólar con las cifras de intereses pagados de (a).
Y la palabra final: realmente no importa qué tasa calcules: ¡lo importante es que al pagar la hipoteca antes, solo estarías pagando un poco más de $7k en lugar de más de $116k en intereses!
1 https://www.bankrate.com/calculators/mortgages/loan-calculator.aspx.
2 https://www.calculator.com.my/fd-savings. La calculadora de depósitos fijos muestra las cantidades en Ringgits malasios (RM), pero eso no importa para nuestros propósitos: solo nos interesan los números.



51 votos
La forma en que calculas "tasa anual" no es la forma de calcular la tasa anual. La fórmula es incorrecta y por lo tanto el resultado es insignificante.
0 votos
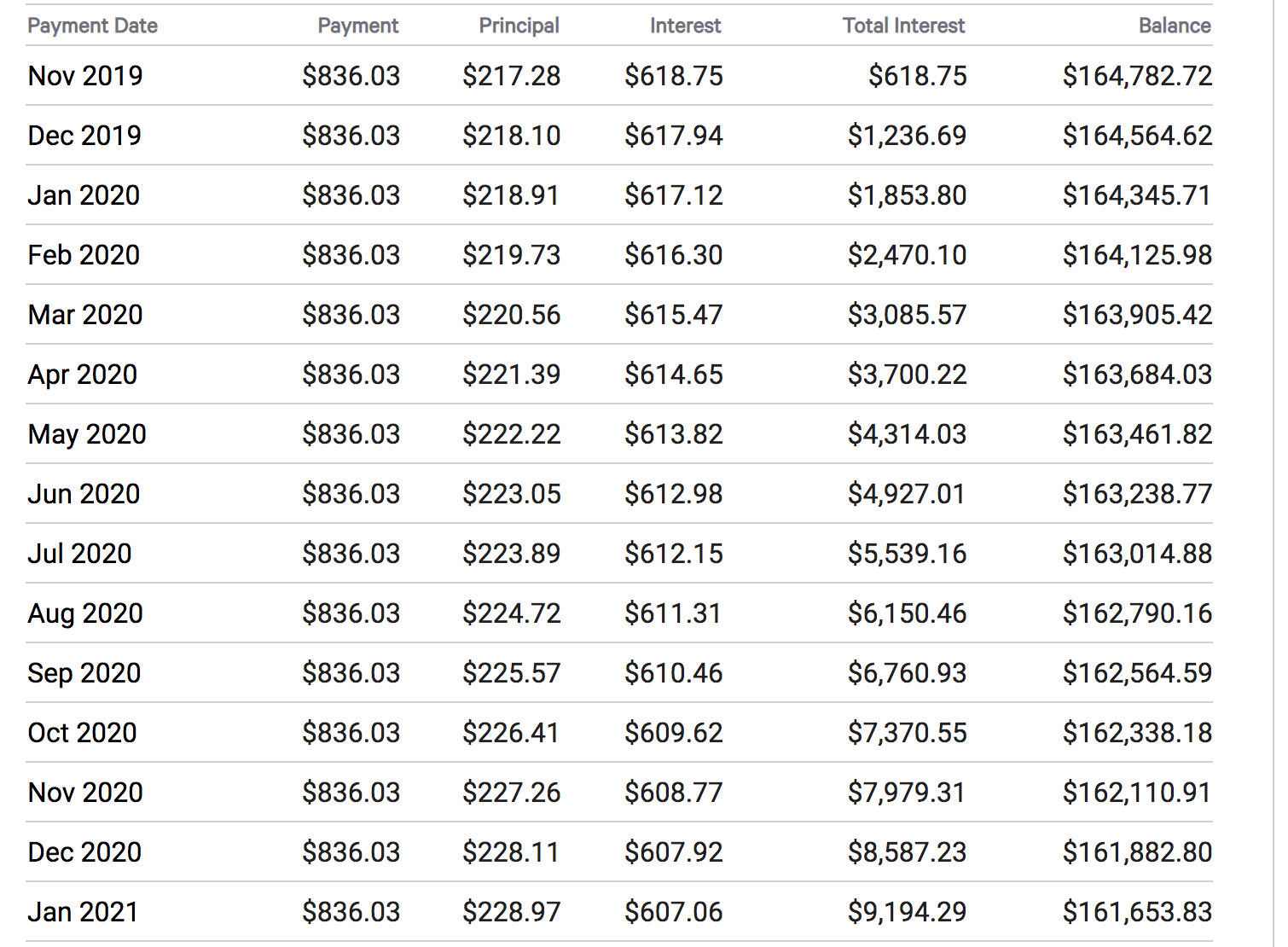
Su tabla de amortización muestra un interés total de $7,370.55 después de los primeros 12 meses, su cifra es a partir del mes 13.
1 votos
@void_ptr ¿Te importaría explicar más?
0 votos
@HartCO ok, pero eso da 4.47% que todavía es mayor que 2.71%
25 votos
El hecho de que termines con una tasa anual diferente a la tasa anual, debería decirte algo ;-) No estás calculando eso correctamente.
4 votos
7,979.31 / 165,000 = 4.84% esto está mal. No puedes usar el saldo original en el denominador. El interés se calcula mensualmente, necesitas calcular mensualmente o tomar el saldo promedio del año.
9 votos
Aunque tengas razón, no estás considerando todos los años en los que no estás pagando ningún interés. Por lo tanto, es alto interés por 1 año, cero por 19 años, versus un interés más bajo por 20 años.
0 votos
No estoy seguro si es relevante y/o tal vez común, pero al menos aquí en Europa del Este, si pagas tu hipoteca antes, estás exento del resto de los pagos de intereses. Es decir, si te quedan 10 años de hipoteca (capital + intereses). Pagas el capital temprano -- el banco tiene que renunciar al resto de los intereses.
1 votos
@Gnudiff Como no pediste prestado dinero en ese momento, no habría razón para que pagues intereses. Solo pagas intereses sobre el dinero que has pedido prestado mientras lo estás devolviendo.
2 votos
@DavidSchwartz Pensé que era normal, sí, pero al menos hace unos 10 años los bancos aquí querían que les pagaras parte de los intereses incluso con la finalización anticipada, hasta que se les prohibió hacerlo por el regulador.