El interés compuesto continuo solo marca una gran diferencia en tasas nominalmente superiores al 5%

Question

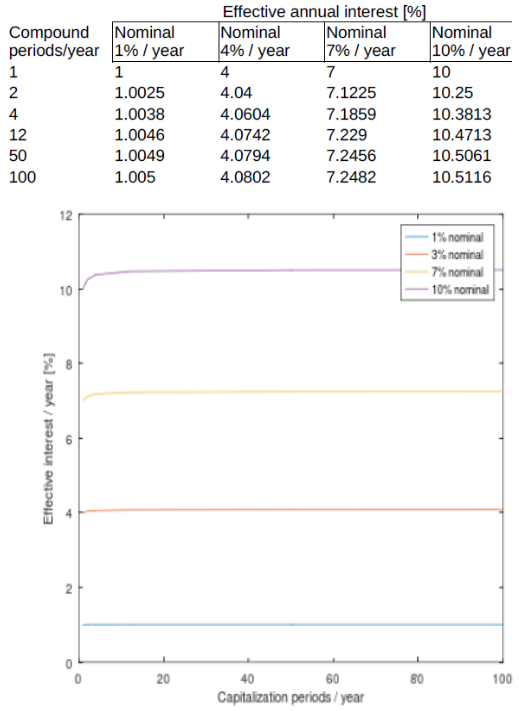
Intenté tener una idea de cuánta diferencia hay cuando una tasa de interés anual nominal se capitaliza varias veces al año, especialmente a medida que el número de capitalizaciones se acerca a infinito, es decir, la capitalización continua. Calculé las tasas de interés anuales efectivas para tasas nominales del 1%, 3%, 7% y 10%. El número de capitalizaciones / año fueron 1, 2, 4, 12, 50 y 100. 100 es cuando la curva se aplana, por lo que es un buen proxy para la capitalización continua (capitalizaciones infinitas / año).

Parece que múltiples capitalizaciones / año solo comienzan a marcar una diferencia significativa para tasas de interés nominales de 5+% / año. ¿Te parece razonable?

Código Matlab/Octave

cCapPrYr = [ 1 2 4 12 50 100 ]'; % Columna de períodos de capitalización/año
rNomInt100 = 1:3:10; % Fila de interés nominal [%]
EffInt100 = zeros( length( cCapPrYr ), 0 );
for NomInt = rNomInt100 / 100
   EffInt100 = [ EffInt100 100*( ...
      ( 1 + NomInt ./ cCapPrYr ) .^ cCapPrYr - 1
   ) ];
end % para NomInt100

plot( cCapPrYr, EffInt100 )
xlabel('Períodos de capitalización / año')
ylabel('Interés efectivo / año [%]')
leyenda('1% nominal','3% nominal','7% nominal','10% nominal')

EffInt100
%    1.0000    4.0000    7.0000   10.0000
%    1.0025    4.0400    7.1225   10.2500
%    1.0038    4.0604    7.1859   10.3813
%    1.0046    4.0742    7.2290   10.4713
%    1.0049    4.0794    7.2456   10.5061
%    1.0050    4.0802    7.2482   10.5116.
%
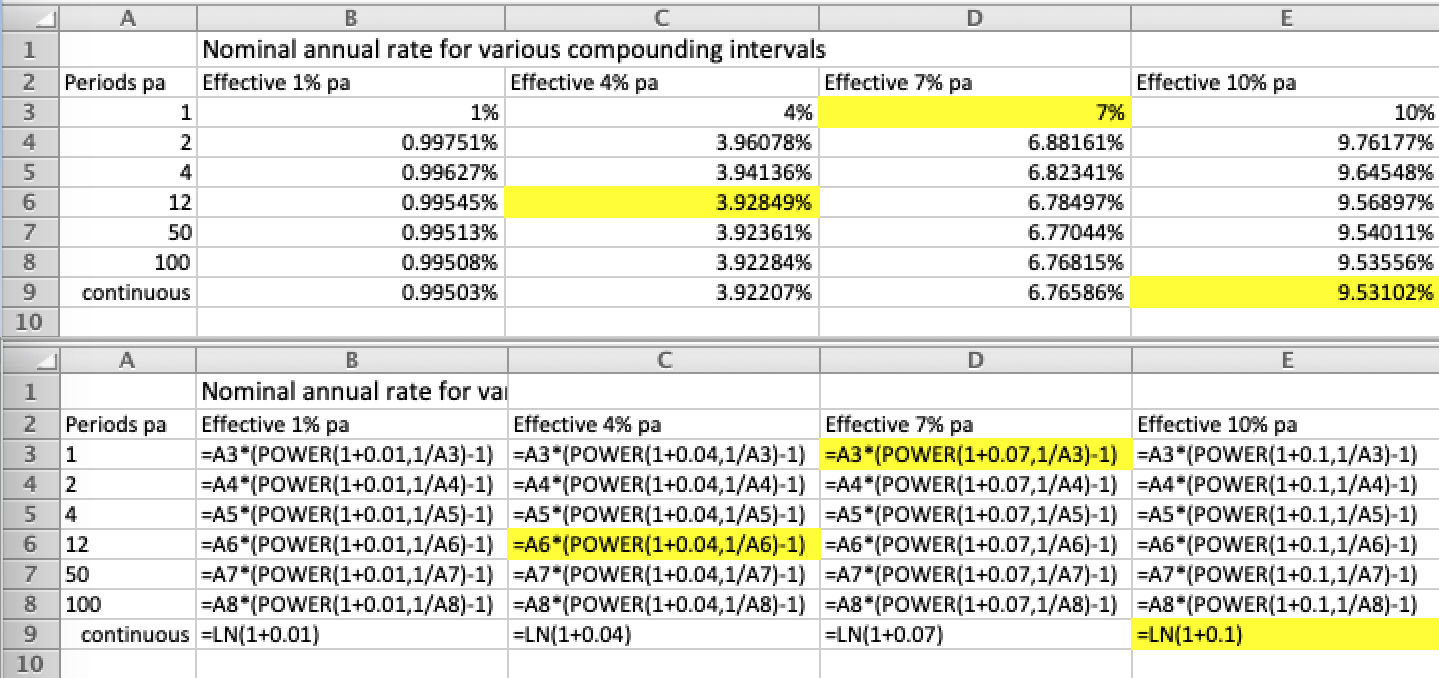
% Importado en LibreOffice Calc, el PDF impreso debe recortarse:
% pdfjam --keepinfo  --trim "2.5in 8.3in 1.5in 1in" --fitpaper true \
%  EffIntVsCapsPrYr.pdf --outfile EffIntVsCapsPrYr-jam.pdf

Answer 1

Tu matemática cuadra.

En la práctica, sin embargo, la 'compensación' continua se utiliza básicamente con fines teóricos únicamente, y solo como un atajo para planificadores financieros y similares. (Las matemáticas involucradas en el interés compuesto continuo son más fáciles que el compuesto por segundo).

Dado que la compensación diaria es básicamente indistinguible de la compensación continua para cualquier tasa de rendimiento plausible, es suficiente - y comparativamente simple de implementar, reduciendo así los costos de transacción - para virtualmente todos los propósitos. Si bien menos períodos de reinversión serían ventajosos para las instituciones financieras, la competencia asegura que ofrecerán las tasas / términos que atraigan a los clientes hasta que el costo de adquirir nuevos clientes exceda el beneficio de hacerlo.

Dado que los bancos regularmente cierran sus libros en un ciclo diario de todos modos, la compensación diaria se alinea muy limpiamente con las prácticas existentes. Es básicamente una solución perfecta que equilibra los efectos de las matemáticas que ilustras con los intereses de los bancos.

Answer 2

La discrepancia proviene de cómo se calcula la tasa de interés para el subperíodo. Si su tasa de interés anual es del 6%, la mayoría de la gente calcularía la tasa mensual como 6%/12 = 0.5%. Matemáticamente eso está realmente equivocado. La tasa "no compuesta" correcta sería (1+0.06)^(1/12)-1, es decir, la raíz duodécima de 1.06 menos 1, lo que arroja 0.48676% y si se utiliza eso no habrá diferencia entre la capitalización o no.

Para tasas de interés pequeñas, la diferencia entre los dos métodos es bastante pequeña, pero en realidad no estoy seguro de lo que hacen típicamente los bancos.

Answer 3

Re. "¿Esto parece razonable?"

Varias expresiones de interés no deberían producir resultados diferentes si se utilizan correctamente. Las tasas de interés nominales para varios períodos de capitalización pueden calcularse a partir de una tasa efectiva, como se muestra en la tabla a continuación. Deberían indicar su intervalo de capitalización al cotizarlos. Por ejemplo, 3 cálculos de un año utilizando las tasas resaltadas a continuación producen rendimientos consistentes.

$100 al 3.92849% nominal capitalizado mensualmente

$100*(1 + 0.0392849/12)^12 = $104

$100 al 7% nominal capitalizado una vez al año

$100*(1 + 0.07/1)^1 = $107

$100 al 9.53102% nominal capitalizado continuamente

$100*e^0.0953102 = $110

Los ejemplos anteriores producen los rendimientos esperados para 4%, 7% y 10% anual efectivo.

Más ejemplos

Aplicando capitalización continua, por ejemplo, durante cinco años al 10% efectivo anual utiliza la conocida fórmula A = e^(rt), por ejemplo

$100*e^(0.0953102*5) = $161.051

y el mismo resultado se produce con 9.54011% nominal capitalizado en 50 períodos al año

$100*(1 + 0.0954011/50)^(50*5) = $161.051

Las tasas nominales generalmente no suelen cotizarse como decimales tan extraños arriba, por ejemplo, es más probable ver "10% nominal capitalizado mensualmente", pero entonces eso no devuelve el 10% efectivo anual, ni es lo mismo que el 10% nominal capitalizado diariamente.