Tengo que entender una cosa sobre este ejercicio: encontrar el mínimo de $f(x, y) = (x-2)^2 + y$ sujeto a $y-x^3 \geq 0$, $y+x^3 \leq 0$ y $y \geq 0$.
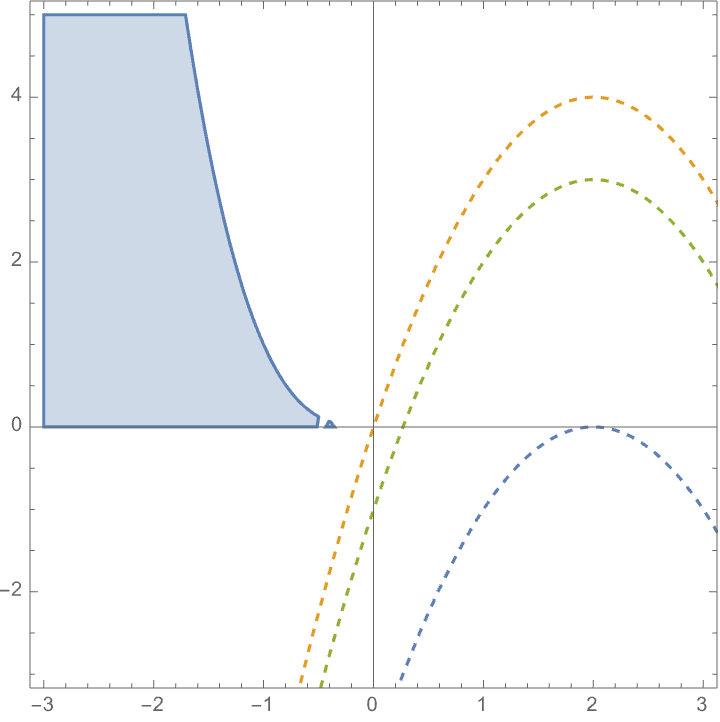
Ahora, resolví el problema bastante fácilmente de forma esquemática: las curvas de nivel de $f(x, y)$ son parábolas cóncavas ($y = k - (x-2)^2$), y la región factible es el plano superior izquierdo delimitado por el eje $x<0$ y debajo de la curva $-x^3$. La solución candidata es $(0, 0)$ en el cual $f(x, y) = 4$.
Por otro lado, quería resolverlo con multiplicadores de Kuhn-Tucker, por lo que planteé el problema en la forma estándar para un problema de mínimo que es:
$$-\max -f(x, y) \qquad \text{sujeto a} \qquad \begin{cases} -y+x^3 \leq 0 \\ y+x^3 \leq 0 \\ -y \leq 0 \end{cases}$$ con Lagrangiano KKT
$$L = -(x-2)^2-y- \lambda(-y+x^3) - \mu(y+x^3) - \Theta(-y)$$
lo que conduce a las condiciones óptimas $$ \begin{cases} -2(x-2) - 3\lambda x^2 - 3\mu x^2 = 0 \\ -1+\lambda - \mu + \Theta = 0 \\ -y + x^3 \leq 0 \quad ; \quad \lambda(-y+x^3) = 0 \\ y+x^3 \leq 0 \quad ; \quad \mu(y+x^3) = 0 \\ -y\leq 0 \quad ; \quad \Theta y = 0 \lambda, \mu, \Theta \geq 0 \end{cases} $$ Desde aquí tengo que estudiar $8$ casos. Aquí hay algunos:
$\bullet$ Cuando $\lambda = \mu = \Theta = 0$ el sistema es imposible.
$\bullet$ Cuando $\lambda = \mu = 0$, $\Theta \neq 0$ obtengo $(2, 0)$ que no cumple con las restricciones.
$\bullet$ Cuando $\lambda = 0$, $\mu \neq 0, \Theta = 0$ obtengo $\mu = -1$ que no es admisible.
$\bullet$ Cuando $\lambda, \mu, \Theta \neq 0$ eventualmente logro obtener entre otros $$\begin{cases} \Theta = \mu + 1 - \lambda \\ (\mu+1-\lambda)y = 0 \end{cases} $$ De lo cual o bien $y =0$ o $\lambda = \mu +1$.
Para $ \lambda = \mu +1$ usando la primera ecuación obtengo $$\mu = \frac{4-2x-3x^2}{6x^2}$$ de lo cual $$\lambda = \frac{4 - 2x + 3x^2}{6x^2}$$ Si $y = 0$ entonces de la ecuación de complementariedad $\mu(x^3-y) = 0$ obtengo $(4-2x-3x^2)x = 0$, por lo tanto o bien $x = 0$ o bien $x = \frac{1}{3}(-1\pm \sqrt{13})$, pero estos últimos no cumplen todas las restricciones.
Por otro lado, $x = 0$ sería bueno si no fuera por el hecho de que no puedo tomarlo porque haría que $\lambda, \mu$ carezcan de sentido.
Entonces te pregunto: ¿cómo lidiar con este problema de manera analítica? Parece que las condiciones de KKT podrían no cumplirse, pero no estoy seguro de esto. ¡Me gustaría otros pares de ojos/mente de tu parte, gracias!
Aquí también está el esquema, con el código de Mathematica. No es tan bueno como pensaba, ya que la región factible debería incluir una porción faltante (el origen a la izquierda y arriba).
plot1 = RegionPlot[{y - x^3 >= 0 && y + x^3 <= 0 && y >= 0}, {x, -3,
3}, {y, -3, 5}, Axes -> True]
plot2 = Plot[{-(x - 2)^2, 4 - (x - 2)^2, 3 - (x - 2)^2}, {x, -3, 5},
PlotStyle -> {Dashed, Dashed, Dashed}]
Show[plot1, plot2]Segundo pensamiento
O tal vez solo podría decir que $y \leq -x^3$ es lo mismo que $-y \geq x^3$ pero esto, con la otra condición implica $\begin{cases} x^3 \leq -y \\ x^3 \leq y \end{cases}$ podría simplemente implicar que o bien $x = 0$ y luego $y = 0$, o bien $y = 0$ y $x$ debe ser negativo, aunque en este último caso seguímos aumentando el valor de $f$ en lugar de encontrar el mínimo.
Tercer Pensamiento
Tal vez olvidé la regularidad de las restricciones. La matriz Jacobiana efectivamente lee
$$\mathsf{J} = \begin{pmatrix} 3x^2 & -1 \\ 3x^2 & 1 \\ 0& -1 \end{pmatrix}$$
De lo cual observamos que en $(0, 0)$ perdemos la regularidad de las restricciones, siendo $\mathsf{J}$ de rango $1$.
Tal vez esto sea lo que hace que las condiciones KKT no se cumplan.
En cualquier caso, el problema con la solución $x = 0$ sigue en pie: no es válida ya que hace que $\lambda, \mu$ carezcan de sentido.
Cuarto Pensamiento
Al analizar el caso en el que solo $\Theta = 0$ puede haber llegado a la solución $(0,0)$, que ahora no presenta ningún comportamiento extraño para $\mu$ y $\lambda$.
La duda sobre las condiciones KKT aún persiste, pero quizás efectivamente sea la falta de regularidad de las restricciones la respuesta, que ocurre en $x = 0$ y $y =0$.
Quinto Pensamiento
No me di cuenta antes, pero la solución $x = 0$, $y =0$ hace que el sistema de gradiente sea imposible: la primera ecuación sería $4 = 0$.
En este punto no tengo más ideas sobre este ejercicio...
Sexto Pensamiento
Tal vez deba pasar a las condiciones de Fritz John, que con un multiplicador más directamente en la función objetivo hace que las cosas tengan sentido. De hecho tendría
$$-2T(x-2)^2 + 3\lambda x^2 = 0$$
Lo cual devuelve $T = 0$ (admisible, ya que necesitamos $T\geq 0$) cuando $x = 0$. Esto pondría una buena piedra de paz sobre esta pregunta, pero aún estoy abierto a posibles respuestas (más rigurosas), ¡así que siéntete libre de comentar!