No es simplemente oferta y demanda. Había oferta y demanda de opciones antes de octubre de 1987, sin embargo, las opciones se negociaban principalmente sin sesgo. La oferta y la demanda juegan un papel, pero es una consideración secundaria.
La volatilidad implícita es una manera de convertir el precio de una opción en un número comparable (anualizado, por ejemplo). La teoría para construir vol es basada en el mundo de Black Scholes (sus suposiciones). Eso es válido para todo tipo de mercados. Si se construyen superficies de volatilidad a partir de mercados de acciones (principalmente estadounidenses y cotizadas en precio), generalmente se elimina el factor americano de la opción antes de construir una superficie de volatilidad. Muchos mercados OTC (por ejemplo, tasas, FX) cotizan principalmente directamente en VI.
Black Scholes implica rendimientos de acciones normalmente distribuidos, mientras que los rendimientos reales de las acciones tienen una asimetría negativa y colas más gruesas debido a que:
-
las acciones (o otros activos subyacentes) tienden a bajar más rápido de lo que suben, por lo que el lado izquierdo tiene una cola más gruesa que el lado derecho, conocido como sesgo
-
los movimientos extremos de precios en ambas direcciones (llamados valores atípicos) son más comunes de lo que sugiere la distribución normal, por lo que ambas colas son más gruesas de lo que una distribución normal sugeriría, conocido como curtosis
Los traders utilizan diferentes volatilidades para fijar precios en opciones (sobre acciones) donde los rendimientos tienden a moverse de manera diferente a lo que sugiere la distribución normal, para representar más fielmente el movimiento de las acciones.
El FX es la forma "más limpia" en la que se cotizan las volatilidades en mi opinión. Las comillas vienen en formatos ATM DNS (delta neutral straddle), RR (Risk Reversals) y BF (Butterflies). Las capturas de pantalla a continuación ignorarán unas cuantas tecnicidades; ATMD no será 50D como sugiere el ejemplo estilizado, y se explica aquí. La VI en sí misma afecta el valor de delta y muchos pares de divisas se cotizan con el prima del delta incluida. BF en sí mismo puede cotizarse de forma diferente.
En resumen,
- ATM determina el nivel (puedes pensar en ello como la VI de Black Scholes para un plazo específico),
- RR el sesgo (hacia dónde se inclina, hacia las opciones OTM en el siguiente ejemplo) y
- BF la curtosis (qué tan pronunciadas son las alas generales).
Utilizando un método algo simplificado de Malz, se puede demostrar rápidamente esto con unas pocas líneas de código en Julia.
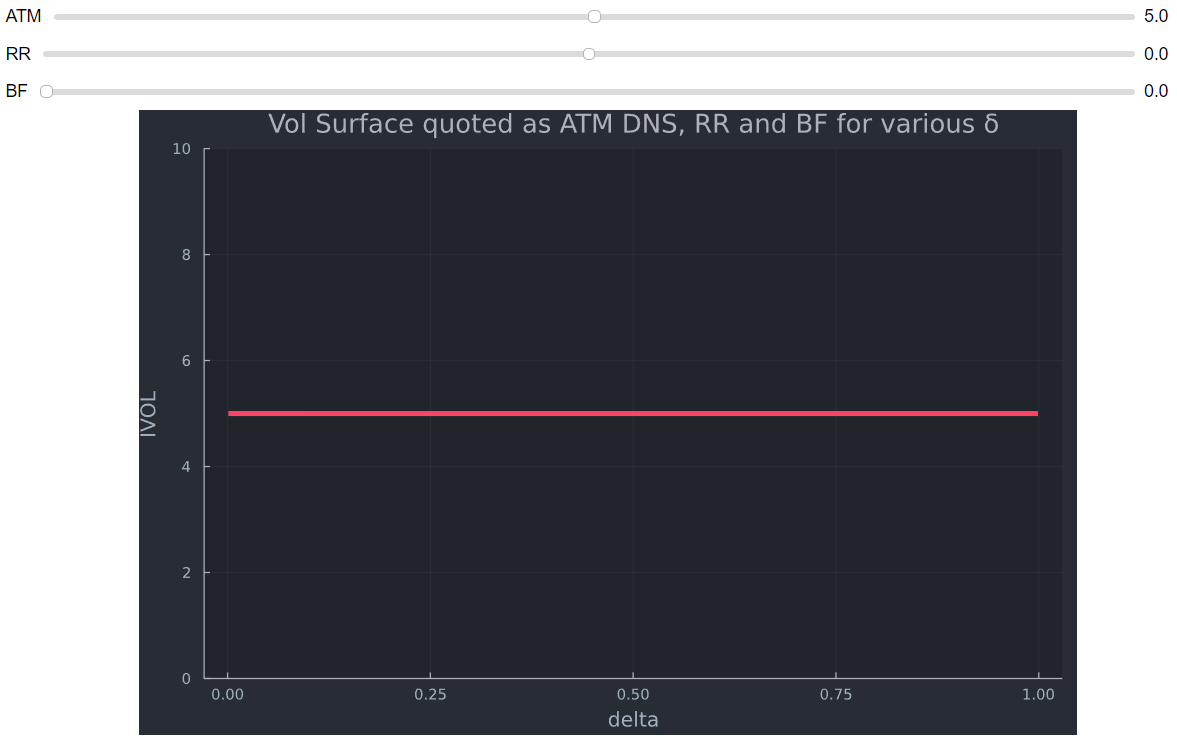
Black Scholes se ve así (RR y BF establecidos en 0). ![ingresa la descripción de la imagen aquí]()
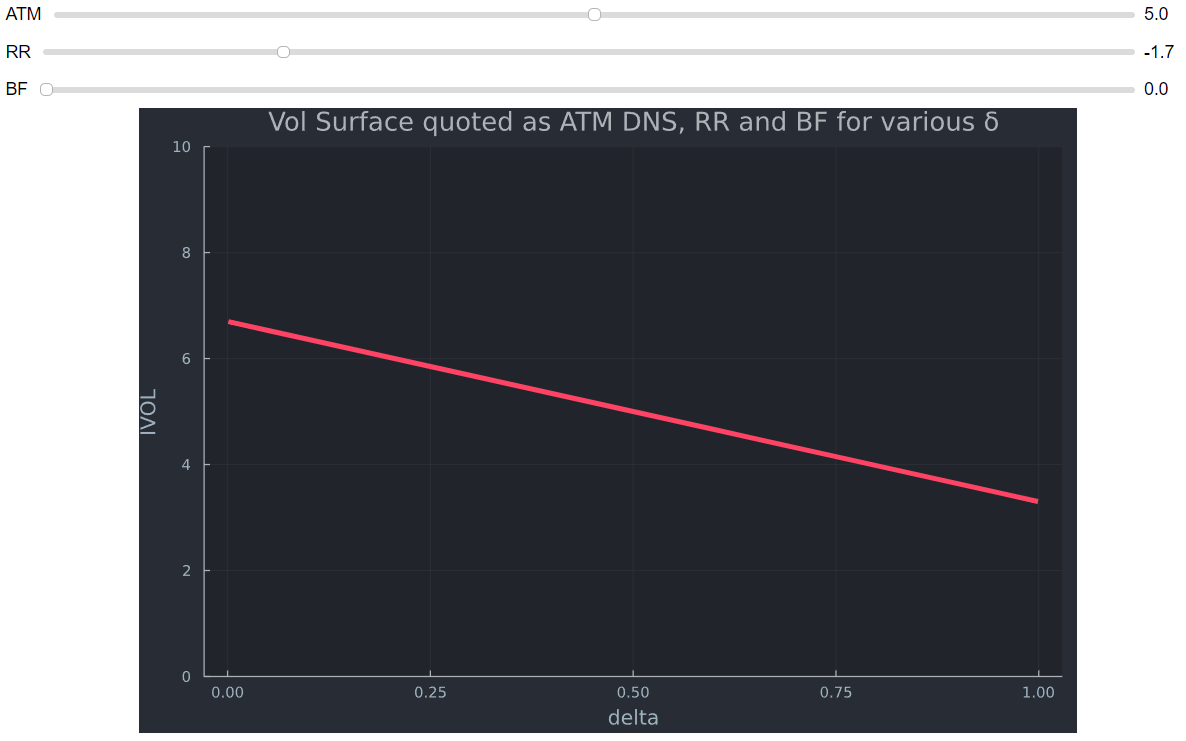
Un RR de 25D se cotiza como volatilidad de la llamada de 25D - volatilidad de la put de 25D; $RR_{25D}=C-P $. Si las opciones OTM puts son más caras (mayor volatilidad), significa que el RR es negativo y la superficie de VOL es mayor para las puts OTM (a la izquierda).
![ingresa la descripción de la imagen aquí]()
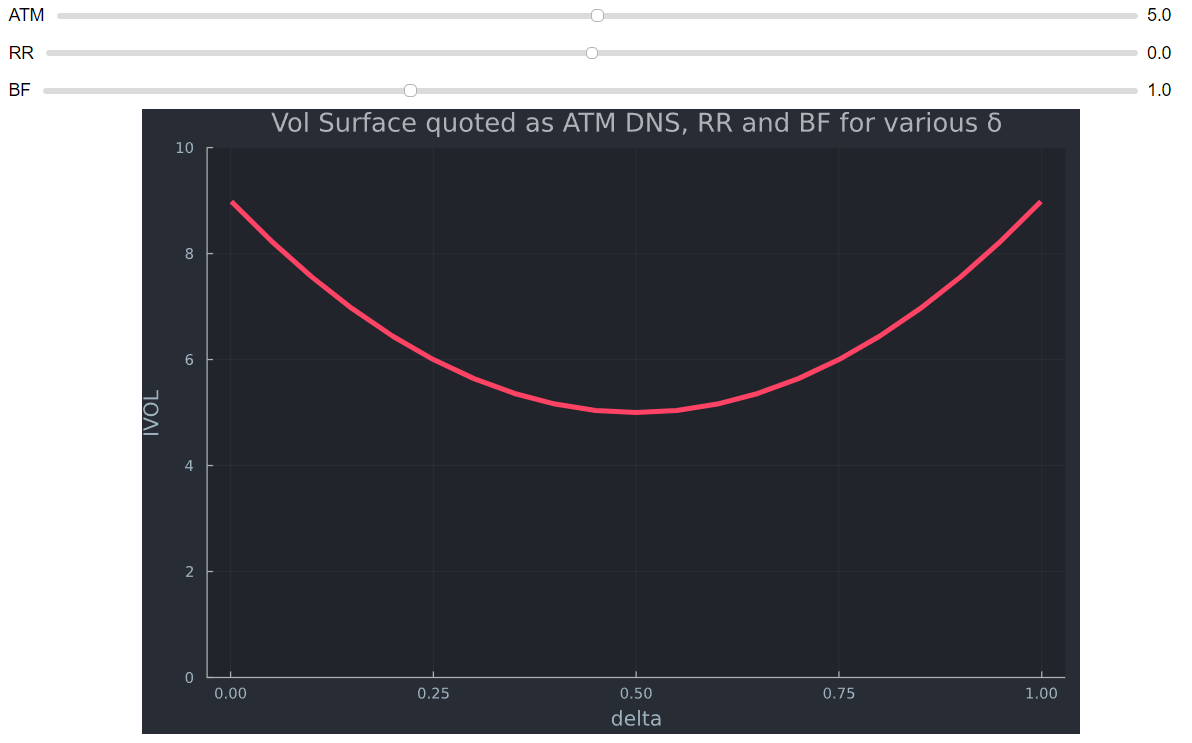
Un BF de 25D se cotiza como $BF_{25D}=((C+P))/2-ATM $ en la comilla de volatilidad. Si el promedio de las volatilidades de la llamada y la put es mayor que ATM (menor es muy raro), se tiene en cuenta la curtosis (colas más gruesas en ambos lados). Aquí establezco RR en cero por conveniencia.
![ingresa la descripción de la imagen aquí]()
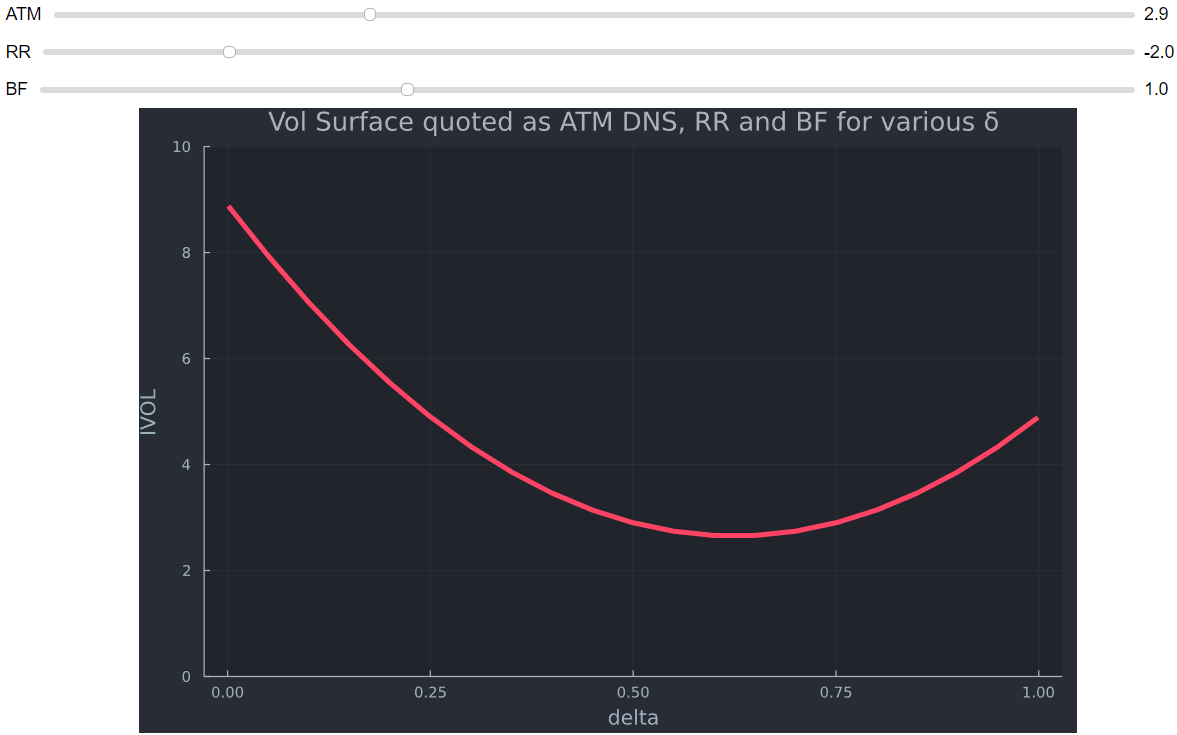
Poniéndolo todo junto se crea la superficie de VOL. ![ingresa la descripción de la imagen aquí]()
Por lo tanto, la superficie de VOL existe principalmente debido a las colas gruesas, la asimetría, la heteroscedasticidad, los saltos (crash), y así sucesivamente. Ninguno de estos fenómenos del mundo real se incluyen en la fórmula de Black Scholes. El mercado simplemente desarrolló formas de tener en cuenta muchas de las deficiencias de Black Scholes.
Todos estos factores (así como la oferta y la demanda) aumentan el precio de mercado de las puts OTM (y calls, dependiendo un poco de los mercados), y por lo tanto se traduce en una mayor volatilidad implícita.