Primero, permítanme decir que a menos que haya otro post, Kevin debería ser aceptado como la respuesta, pero quería agregar una clase de sesgos que están en la literatura, pero no en la literatura de ciencias sociales. En otras palabras, esto es conocido, pero desconocido para los economistas.
Como antecedente, he estado haciendo el argumento técnico de que hay tres tipos de errores matemáticos en la literatura de economía financiera. Dos de esos errores son aplicar matemáticas perfectamente buenas de manera inapropiada.
Como ejemplo, imagina que tú y tu amigo multimillonario acaban de aprender geometría euclidiana. Siempre has amado el postulado de líneas paralelas, mientras que tu amigo está enamorado del Teorema de Lado-Ángulo-Lado. Para probar las ideas de Euclides y demostrar que son correctas, deciden caminar a lo largo de líneas paralelas y medir la distancia entre ustedes al final de la caminata. Necesitas un amigo multimillonario para malgastar la cantidad requerida de dinero para hacer esto.
Para estar seguro de que lo están haciendo correctamente, ambos van al ecuador. Tú te paras en el meridiano y tu amigo se para a noventa grados de longitud. Ambos miran hacia el Norte.
Comienzas tu caminata viajando perpendicular al ecuador y, inesperadamente, ambos llegan al Polo Norte, en líneas paralelas que se intersectan y crean un triángulo de 270 grados donde dos lados son líneas paralelas.
Las finanzas cometen el mismo tipo de error al violar la contraparte del Teorema del Libro Holandés.
El cálculo de Ito asume que todos los parámetros son conocidos. Por supuesto, no lo son. Ahí es donde surge el problema. La finanza teórica y empírica es una disciplina frecuentista. A primera vista, no hay nada de malo en eso, siempre y cuando el trabajo siga siendo teórico y nunca se aplique a algún problema del mundo real.
Este sesgo podría ser llamado sesgo de experto porque solo un experto puede causar este sesgo. Un novato no podría hacer que esto suceda. Es un sesgo debido únicamente a la capacitación. Ha habido advertencias empíricas desde 1963 para abandonar las matemáticas utilizadas en finanzas, pero nadie dejará de hacerlo.
El artículo original de Black y Scholes que establece la modelización de precios de opciones desde entonces tiene un párrafo justo antes del final que afirma que los autores probaron el método empíricamente y no funcionó. De hecho, nunca ha pasado una prueba de validación. Se realizan conferencias completas sobre las anomalías del modelo.
Hay tres dificultades involucradas en la sustitución de estimaciones por valores conocidos y el artículo que estoy a punto de citar implica una de ellas. Este es un problema bien conocido en la literatura matemática y de probabilidad. Tiene que ver con las reglas de matemáticas de probabilidad a un nivel más profundo en el que un economista jamás sería entrenado. Por lo tanto, nunca aparece en la formación en ciencias sociales. Irónicamente, es importante en el campo de la filosofía. Hay filósofos, así como matemáticos y probabilistas que escriben sobre este tema. El único lugar donde sería vital, las finanzas, ha estado prácticamente en silencio desde que Markowitz publicó. Solía ser parte de la economía. De hecho, un ganador del premio Nobel escribió al respecto.
Así que aquí está el problema, no parecerá un problema, lo cual también es parte del problema.
Esta es la tercera axiomática de Kolmogorov. P left( bigcup i=1inftyEi right)= sum inftyi=1P(Ei)P left( bigcup i=1inftyEi right)= sum inftyi=1P(Ei)
Al final, simplemente permite a la persona que crea un modelo cortar una función de densidad acumulada en infinitas partes, incluyendo partes que no son atómicas. Pueden ser arbitrariamente pequeñas. A los economistas les encanta llevar las cosas hacia el infinito o el cero.
Este es el tercer resultado de de Finetti del Teorema del Libro Holandés. P left( bigcupNi=1Ei right)= sumNi=1P(Ei)P left( bigcupNi=1Ei right)= sumNi=1P(Ei)
Esto básicamente establece que no puedes tener partes no atómicas. No puedes volverte arbitrariamente pequeño. Puedes volverte extremadamente pequeño, pero debes permanecer atómico.
¿"Y qué" preguntas?
Bueno, a menos que tengas un número infinito de clientes, no modelar como si los hubiera, solo si realmente los hay, entonces no hay dificultad creada por el uso de los axiomas de Kolmogorov. Sin embargo, para cualquier número finito de participantes, las distribuciones de probabilidad frecuentistas dan lugar a pérdidas seguras si sabes cómo hacer que sucedan.
Esto no es un secreto. Leonard Jimmie Savage coescribió un libro sobre esto antes de Black-Scholes y la finalización de los diversos CAPM y el APT. Esto es una forma de comportamiento de manada. Todos saben que algo no funciona, pero no dejan de hacerlo.
El artículo está escrito en un estilo similar a Cálculo de la forma fácil. Hay imágenes pero no matemáticas formales. Hay un campo de probabilidad, filosofía y matemáticas dedicado a este problema que ya existe. Este artículo es similar a una prueba de concepto. Está destinado a mostrar una patología específica, pero no es el conjunto exclusivo de patologías. He encontrado cinco de ellas que suceden en finanzas empíricas.
Este sesgo es similar a los físicos que siguen utilizando éter luminífero mucho después de que los experimentos de Michelson y Morely demostraran que no podía existir. También es similar a los médicos que rechazaron la teoría de los gérmenes a pesar de la evidencia. Es un tipo específico de sesgo. Lo menciono porque los sesgos no son solo para aficionados. Se necesitaron profesionales para estrellar el transbordador espacial, dos veces, en accidentes prevenibles.
El artículo está aquí. Está en Internet Archive porque el sitio web del blog fue comprado por otra empresa.






0 votos
Por favor, no olvides el error meta: la creencia de que el conocimiento de los errores de inversión más comunes te protege de cometer errores de inversión tú mismo o incluso te permite aprovechar los errores de otras personas.
0 votos
@quarague Gracias por tu comentario, sin embargo, la explotación de cualquier sesgo está más allá de mis intenciones. Dejaré eso a Fuller Thaler Asset Management fullerthaler.com/about
0 votos
¿Quién dice que la "sobrediversificación" es un error? Si le preguntas a Warren Buffet, deberías poder hacerlo muy bien con 20 "golpes" a tus compras de por vida. Simplemente no deberías comprar sin investigar primero.
0 votos
@Sablefoste Creo que es demasiado confiado asumir que el Joe promedio tiene las mismas habilidades que Warren Buffet.
0 votos
@T123, estoy de acuerdo en que la mayoría no tienen la habilidad de Warren Buffet. Pero el punto era que la "sobrediversificación" no es un error o un problema sistemático. La pregunta asumió que era un problema "conocido" (como lo hizo al menos una de las respuestas) cuando de hecho es exactamente lo opuesto para un inversor experimentado. Creo que para que algo sea clasificado como un error, debe mostrar que el comportamiento casi siempre resulta en pérdida de capital (como comprar alto y vender bajo).
0 votos
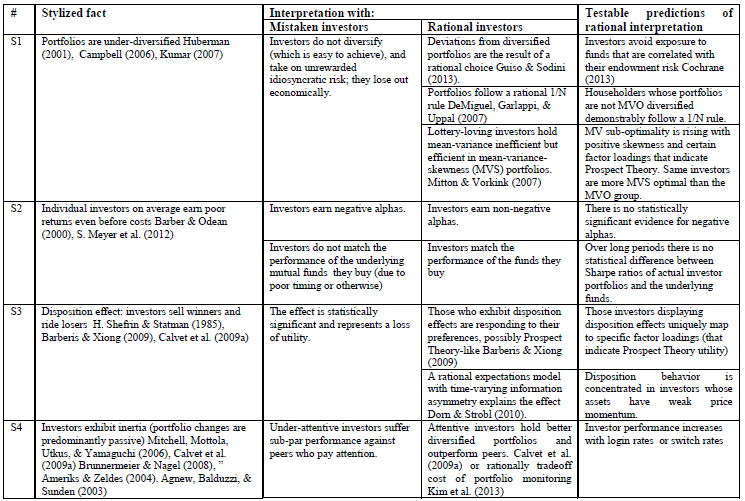
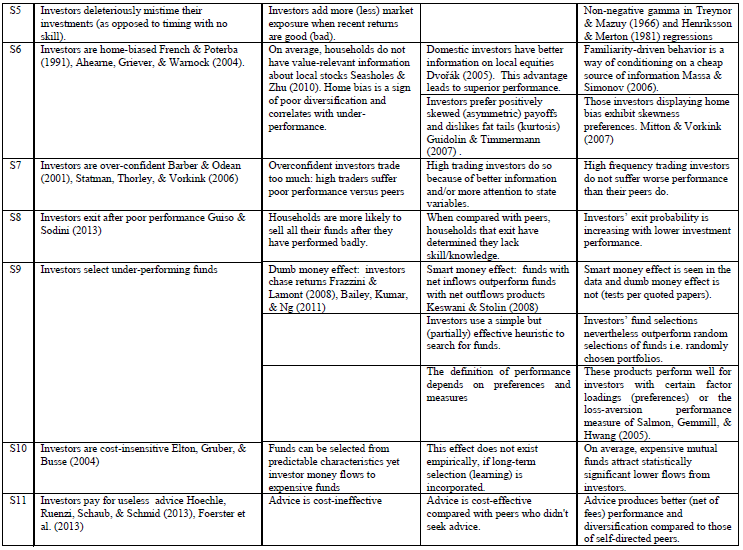
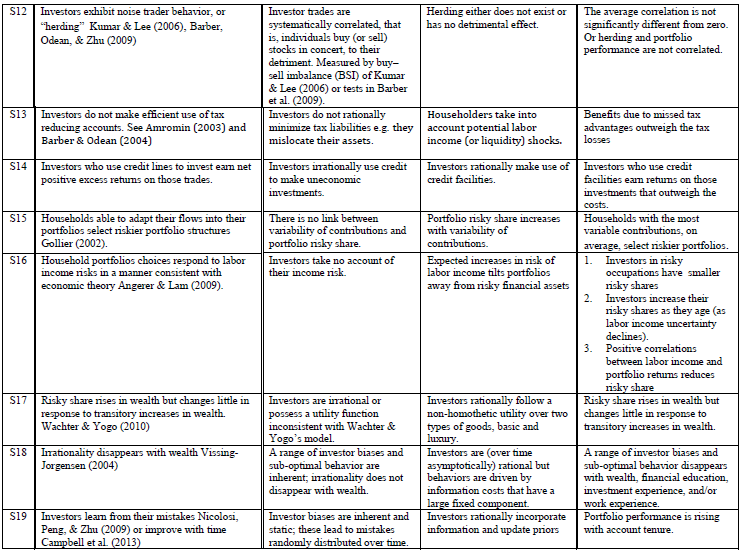
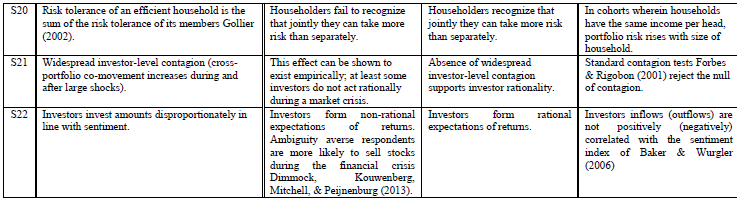
Bueno, si echas un vistazo a los periódicos entonces verás que la respuesta depende (como siempre). Hay motivos racionales e irracionales para la subdiversificación. La literatura en BFin., sin embargo, lo considera un error de inversión. Dejemos que los lectores decidan si lo es o no, ¿estamos de acuerdo?